Landau-Theorie der Phasenumwandlung von Membranen

Appendix 10 A: Landau-Theorie der Phasenumwandlung von Membranen

Vorbemerkung
Um Einblick in die thermodynamischen aber auch strukturellen Eigenschaften von Lipidschichten zu erhalten, ist die klassische Landau-Theorie immer noch sehr hilfreich; Vor allem für den Experimentator. Sie liefert Vorschriften zur Untersuchung der Ordnung der Phasenumwandlungen oder zur Messung physikalischer Eigenschaften der Membranen. Außerdem gibt sie Einblick in die durch Lipide vermittelte Protein-Protein-Wechselwirkung oder ermöglicht Abschätzungen der Wirkung lokaler Fluktuationen des Ordnungsparameters. Jedoch versagt sie bekanntlich bei kritischen Phänomenen, die wir nur kurz betrachten werden.

Ausgangspunkt der Landau-Theorie (s. Landau und Lifschitz, Band V) ist die Entwicklung der freien Enthalpie in Potenzreihen eines geeigneten temperatur- und druckabhängigen Ordnungsparameters $\eta (\pi ,T)$

$G(\pi , T , \eta)=G_0 + \sum_n A_n (\pi , T) \eta^n+\frac{1}{2} \beta (\pi , T) \nabla \eta^2$ (10A.1)

$G_0$ ist die freie Energie der Phase mit der niedrigeren Symmetrie, d.h. in unserem Fall der $L_\alpha$ -Phase. Der letzte Term mit $\nabla \eta^2$ ist notwendig, um Effekte der Grenzflächen zwischen zwei Lipidphasen zu behandeln oder die lipidvermittelte Wechselwirkung zwischen Proteinen zu beschreiben (s. § 9-11).

Die Wahl des Ordnungsparameters hängt von der Fragestellung ab.

- Zur Beschreibung der Phasenumwandlungen ohne Änderung der Neigung der Lipide benutzt man den mittleren Ordnungsgrad S der Gl. 10A.1.

- Um die kollektive Neigung der Ketten (z. B. in der $L_\beta$ ’-Phase oder in der Umgebung von Proteinen) zu berücksichtigen, wird der Ordnungsparameter:
$\Omega ( \vec{r} ) =\Theta ( \vec{r} ) \Theta_0$

eingeführt, wobei $\Theta(\vec{r})$ bzw $\Theta_0$ die Neigungswinkel in den Phasen niedrigerer bzw. höherer Symmetrie sind.

- Um Änderungen der Symmetrie der lateralen Ordnung zu berücksichtigen, benutzt man normalerweise die laterale Dichte $\rho(\vec{r})$ . Es ist jedoch auch oft günstig, $\rho(\vec{r})$ durch die reduzierte Fläche pro Molekül zu ersetzten (J. C. Owicki, M. W. Springgate, and H. M. McConnell (1978), Proc. Natl. Acad. Sci. USA 75, 1616).

$\eta(\vec{r})=\frac{A(\vec{r}-A_f}{A_f-A_c}$ (10A.2)

wobei $A(\vec{r})$ die molekulare Fläche pro Lipid in einem Zwischenzustand und $A_c$ bzw. $A_f$ die entsprechenden Werte in der kristallinen (niedrige Symmetrie) bzw. fluiden Phase ist.

Alternativ kann man schließlich auch die Dicke der Membran als Ordnungsparameter nehmen. Die einfachste Bedingung für das Auftreten einer Phasenumwandlung ist der Umschlag des quadratischen Terms (in der Summe) von einem positiven zu einem negativen Wert, und zwar bei einer Umwandlungstemperatur T*. Daher macht man den Ansatz:

$A_2= a(T-T^*)$ (10A.3)

Man hat nun zwei Situationen:

- Falls $A_4 > 0$ und alle höheren Terme verschwinden, hat die G- $\eta$ -Kurve nur ein Minimum. Dieses liegt für $T > T^*$ bei $\eta = 0$ (Zustand höherer Symmetrie) und für $T < T^*$ bei $\eta_0 = \sqrt{\frac{A_2}{2A_4}}$ . Die Umwandlung ist kontinuierlich, d.h. von zweiter Ordnung.

- Falls $A_4 < 0$ ist, benötigt man einen Term 6. Ordnung (um $G (\eta )$ positiv zu halten). Wie Abb. fig.10.A.1 zeigt, gibt es zwei Umwandlungstemperaturen: $T_t$ und $T^*$ . Bei $T = T_t$ sind die Minima (von denen eines bei $\eta = 0$ liegt) gleich tief, und man befindet sich im Zentrum der Umwandlung. Bei $T < T_t$ ist die Phase niedriger Symmetrie stabil.

Allerdings muss der Übergang aktiviert werden und ein spontaner Übergang erfolgt erst bei $T = T^*$ . Die Umwandlung besitzt somit eine Hysteresis (s. Abb. fig.10.A.1), und es gibt Koexistenz zweier Phasen.

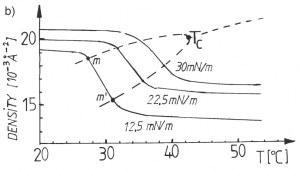
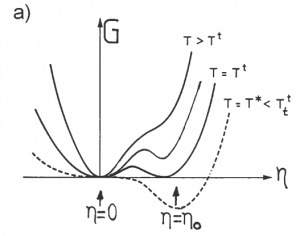
fig.10.A.1 a) Darstellung der Landau-Entwicklung der freien Energie (nach Gl. (10.4)) mit Term zweiter, vierter und sechster Ordnung. Definition der beiden Umwandlungstemperaturen $T_t$ und $T^*$ .
b) Phasenumwandlung der Lipidmonofilme (hier DMPC) an der Luft/Wasser-Grenzfläche dargestellt als Dichte-Temperatur-Diagramm für verschiedene laterale Drücke. Die Geraden
m – m’ markieren die Hauptumwandlung. Die Abnahme ihrer Breite mit zunehmendem Druck zeigt den Umschlag von einer Umwandlung erster zu einer Umwandlung zweiter Ordnung. Da sich die Symmetrie beim Übergang ändert, handelt es sich um einen trikritischen Punkt.
Wir wollen nun die $L_\alpha$ $\rightarrow$ $L_{\beta ^\prime}$ Lipidphasenumwandlung ausführlicher betrachten. Um der kollektiven Neigung der Lipide in der $L_{\beta ^\prime}$ -Phase Rechnung zu tragen, müssen wir zwei Beiträge zur freien Energie berücksichtigen.

- Eine Entwicklung als Funktion des Unterschiedes in der lateralen Dichte

$\Delta G_\rho(\pi,T,\rho)= \frac{1}{2}a(T-T*)\rho^2+\frac{1}{2}A_4(\pi,T)\rho^4+\frac{1}{6}A_6(\pi,T)\rho^6 )$ (10A.4)

- Eine Entwicklung als Funktion der Änderung im Neigungswinkel $\theta$ und ein Kopplungsterm zwischen $\rho$ und $\theta$ gemäß:

$\Delta G_{\theta , \rho}(\pi,T,\rho)= \frac{1}{2} K_{11}$ $( \theta_{\beta}$ – $\theta_{\alpha} ) ^{2}$ $+ C( \pi , T) \rho ^{2}$ $( \theta_{\beta}$ – $\theta_{\alpha} )$ (10A.5)

Der erste Term gibt die Arbeit an, die nötig ist, um die Kettenorientierung lokal zu ändern (z. B. von $\theta =0$ um den Neigungswinkel der Ketten). Daher ist $K_{11}$ gleich dem elastischen Modul der Auffächerung (= Splay-Modul) der Lipidorientierung.

Aus den beiden Beiträgen zur Gesamtenergie $G_\rho$ und $G_{\theta , \rho}$ kann man den Ordnungsparameter $\Omega$ eliminieren, und zwar durch Minimalisierung der Gesamtenergie ( $G = G_\rho + G_{\theta , \rho}$ ). Eine einfache Rechnung liefert:

$\Delta G(\pi,T)=\frac{1}{2}a(T-T*)\rho^2+\frac{1}{4}(A_4- \frac{2t^2}{K_{11}}\rho^4+\frac{1}{6}A_6\rho^6$ (10A.6)

Das entscheidende Ergebnis ist: der Term vierter Ordnung erhält einen negativen Beitrag. Dies hat zwei sehr wichtige und interessante Konsequenzen:

1) $K_{11}$ und $t$ hängen beide vom lateralen Druck in der Membran ab, aber in verschiedener Weise. Es ist klar, dass $K_{11}$ mit zunehmender Dichte $\rho$ (bzw. $\pi$ ) zunimmt. Dagegen nimmt der Kopplungsterm $t$ ab, denn wenn $\rho$ zunimmt, wird der Dichteunterschied bei der Hauptumwandlung kleiner. Dies hat zur Folge, dass bei kleinen Drücken der Term vierter Ordnung negativ wird ( $K_{11}$ ist klein). Daher ist ein Term sechster Ordnung nötig, und die Umwandlung ist erster Ordnung. Bei großen Werten von wird $A_4$ positiv und die Umwandlung wird von zweiter Ordnung.

Tatsächlich wurde dieser Wechsel in der Ordnung der Umwandlung bei Monoschichten beobachtet, wie Abb. fig.10.A.1 zeigt. Ähnliche Umschläge von erster zu zweiter Ordnung mit zunehmendem Druck wurden auch in nematisch-smektisch A-Übergängen beobachtet, sowie beim Übergang ferromagnetisch-paramagnetisch, wobei man auch vom Rodbell-Bean-Effekt spricht (s. Albrecht, et.al. (1978) Journal de Physique. 39, 301). Ohne Landau-Theorie könnte man solche Umschläge in der Ordnung der Umwandlung nicht verstehen.

2) Ein weiterer Vorteil der Landau-Theorie ist, dass die Entwicklungskoeffizieten $A_n$ gemessen werden können. So erhält man das Verhältnis $\frac{a^2}{A_4}$ aus dem Sprung des thermischen Ausdehnungskoeffizienten oder der lateralen Kompressibilität bei der zweiter Ordnung Umwandlungen (s. Albrecht et al., 1978).

Falls $A_4$ , $A_6$ und $t$ nicht stark von der Temperatur abhängen, kann man den Koeffizienten $a$ direkt aus der Übergangswärme $\Delta H_t$ und der Änderung der Dichte $\Delta \rho_t$ bestimmen, gemäß: