Lösungen Kapitel 10

From BioPhy.de Wiki

Aufgabe 10.1:

Lipid Monofilme:

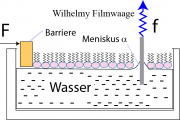
(i) Messung des Drucks mittels Wilhelmy Filmwaage: Diese besteht in der Regel aus einem Platinplättchen, das in den Trog eintaucht. Es wird durch Kapillarkraft aus dem Wasser gezogen. Die auf das Filterpapier wirkende Kraft ergibt sich aus der Balance zwischen Gravitation und Kapillarkraft (Oberflächenspannung):

$LaTeX: F=mg+2\sigma(a+b)cos(\alpha)-\rho ghab$

Dabei sind a: Dicke; b: Breite (a << b); h die in die Subphase eingetauchte Länge des Plättchens, g die Gravitationskonstante und $LaTeX: \rho$ die Dichte der Flüssigkeit. In der Regel kann man durch Wahl der Plättchen vollständige Benetzung erreichen ( $LaTeX: \alpha$ = 0° ). Durch Wahl sehr dünner Plättchen (a << b) wird a $LaTeX: \approx$ 0 und man kann auch den Auftrieb vernachlässigen. Daher folgt:

$LaTeX: F=mg + 2\sigma b cos(\alpha)$

Dadurch erhält man durch Messung der Kraft direkt die Oberflächenspannung $LaTeX: \sigma$ . F wird durch eine Federwaage bestimmt. Der laterale Druck p (in $LaTeX: \frac{mN}{m}$ gemessen) ist durch die Differenz zwischen der Oberflächenspannung des Wassers ( $LaTeX: \sigma_0$ ) und der mit der Lipidschicht bedeckten Oberfläche (s) bestimmt: $LaTeX: \pi=\sigma_0-\sigma$ .

Schematische Darstellung der Filmwaage mit Wilhelmi Filmwaage.

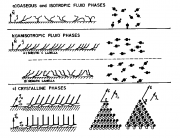
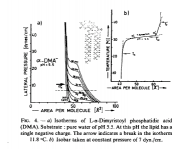
Der Polymorphismus monomolekularer Lipidfilme: Lipidmonofilme sind 2D flüssigkristalline Zustände und werden durch zwei Ordnungsparametern bestimmt: Die in Orientierung der Ketten (die in Kapitel 10.3 definiert wurde) und die laterale Packung der Lipide $LaTeX: \rho(\vec{r})$ . Aus dieser Betrachtung der Ordnungsparameter erwartet man die in der unten wiedergegebenen Abbildung 13 der Arbeit von Albrecht et al (1978) dargestellten Phasenzustände. Man beachte, dass auch die Kopfgruppen geneigt sein können, so dass auch für diese ein Orientierungs-Ordungsgrad eingeführt werden kann.

Lipidphasen

Legende

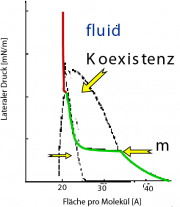
Ein Beispiel, an dem man den thermotropen Polymorphismus der Monofilme gut studieren kann, sind die einkettigen Fettsäuren. Abbildung unten zeigt das Beispiel der Palmitinsäure. Eine Besonderheit ist ist die Umwandlung zwischen dem festen Zustand mit geneigten Ketten (man nennt ihn auch smektisch BC) in den mit normal zur Oberfläche stehen Ketten. Man sieht, die Umwandlung ist im Falle der Fettsäuren von erster Ordnung. Im Ggensatz zu den Phospholipiden, bei denen dieser Übergang von zweiter Ordnung ist, wie der Einsatz b im linken Bild der Abb. 2 zeigt, der nur einen Knick bei der Umwandlungs-Temperatur $LaTeX: T_k$ zeigt.

Abb. 2 Links: a) Druck-Flächen-Diagram von Dimyristoylphsphatidylcholine. b) Isobare, bei konstantem Druck von 7 $LaTeX: \frac{mN}{m}$ aufgenommen. Sie dient der Prüfung, ob die Umwandlung erster oder zweiter Ordnung ist. Rechts: Druck-Flächen-Phasendiagramm von Palmitinsäure mit zwei kristallinen Zuständen I und II mit geneigten bzw. senkrecht zu Oberfläche orientierten Ketten. Die Neigung der Ketten kann mittels Elektronenbeugung der Monoschichten beobachtet werden. Beim Übergang von I nach II geht das hexagonale Beugungsmuster in ein trigonales über.

Aufgabe 10.2:

Elektrisch induzierte Phasenumwandlungen

Vorbemerkung: Durch pH-Änderungen und Ionen induzierte Konformations- und Phasenumwandlugen von Membranen sind aus folgenden Gründen besonders interessant: (i) Sie können isotherm ablaufen und ermöglichen lokale Konformationsumwandlungen, z. B durch Adsorption geladener Proteine wie Annexine (s. Abb 9.4a und 9.b). (ii) Die Umwandlungen besitzen eine ausgeprägte Hysteresis und können möglicherweise als Kurzzeitgedächtnis fungieren (s. dazu Ergänzung am Ende)

Freie Enthalpie: G(T,p,N)=U(V,S,N) +pV -TS $LaTeX: \Delta G = -SdT+Vdp [+\mu dn]$ ;

$LaTeX: A=\frac{\partial G}{\partial \pi} ; S=\frac{\partial G}{\partial T}$ ;

$LaTeX: \frac{d(G_1 - G_2)}{dT}=(\frac{\partial}{\partial T}(G_1 - G_2) + \frac{\partial \pi}{\partial T} \frac{\partial }{\partial \pi})(G_1 - G_2)$

$LaTeX: 0 = -\Delta S - \Delta A \frac{\partial \pi}{\partial T} \frac{\partial}{\partial T}=-\frac{\Delta A}{\Delta S} \Delta T = -\frac{\Delta A \Delta \pi}{\Delta S}$

Ergänzung zur Aufgabe 10.2.:

Hystersis effekte: Hystereseeffekte ladungsinduzierter Konformationsumwandlungen - Domänenbildung.

Hystereseeffekte sind ein allgemeines Phänomen bei ladungsinduzierten Umwandlungen von Membranen Proteinen oder Polyelektrolyten. Hysteresiseffekte in Polyelektrolyten wurden von A. Katchalsky untersucht, der zeiget, dass man damit isotherm arbeitende künstliche Muskeln herstellen kann (s. dazu T. Hill Statistical Thermodynamics Ch.21.4).

Hysteresiseffekte sind jedoch auch von außerordentlichem Interesse als mögliche biologische Schalter oder Kurzzeitspeicher. Ein biologisch interessantes Beispiel ist die Hysterese der pH- oder Ca-induzierten Phasenseparation in Membranen. Ein Beispiel eines in vitro Modells zeigt folgende Abbildung. In diesem Experiment wurde die Temperatur so eingestellt, dass man sich bei pH = 7 mitten in der L $LaTeX: \alpha$ -L $LaTeX: \beta$ -Umwandlung befindet. Der Bruchteil der Lipide in der festen Phase ist als Funktion des pH wiedergegeben und zwar bei steigendem und fallendem pH. Man beobachtet eine ausgeprägte Hysteresis der Umwandlung, die sich über rund 1.5 pH-Einheiten erstreckt.

Hysteresis der ladungsinduzierten Phasenumwandlung in Membranen aus Dipalmitoylphosphatidsäure (DPPA). Bei pH = 8.5 ist das Lipid zweifach negativ geladen und bei der eingestellten Temperatur (bei 20 $LaTeX: \degree$ C) fluide, während es bei pH = 6 einfach geladen und im Gelzustand (L $LaTeX: \beta$ ') ist. Ursache der Hysteresis ist die Bildung von Domänen in Kombination mit dem Unterschied im Oberflächenpotential (und damit des pH) zwischen fluider und fester Phase.

Ursache der Hysteresis ist die in Kapitel 10.23 beschriebene Änderung des pH an der Oberfläche geladener Membranen. Das negative Oberflächenpotential in der fluiden Phase (zweifach negativ) ist höher als in der kristallinen Phase, in der die Lipide nur einfach geladen sind. Bei zunehmendem pH muss man also zu höheren Werten des pH im Volumen gehen, um das Lipid zu dissoziieren und damit die membran zu schmelzen. Umgekehrt muss man bei pH-Abnahme zu niedrigeren Werten des pH gehen, um die Protonen zu binden, da das negative Potential ja geringer wird.

Die durch Ca-Ionen vermittelte Hysteresis könnte bei der Fusion synaptischer Vesikel mit der präsynaptischen Membran eine wichtige Rolle spielen, die durch Ca-Einstrom getriggert werden (s. Aufgabe 9.7). Wie in Aufgabe 9.A1 gezeigt wird, bleiben die lokale Anhäufungen von der Ionen auch bestehen, wenn die Kalziumkonzentration nach der anfänglichen Erhöhung wieder auf den für Zellen im Ruhezustand typischen Wert von 10 $LaTeX: ^{-7}$ M abfällt. Aus heutiger Sicht wird die Fusion der Vesikel mit der präsynaptischen Membran mit großer Wahrscheinlichkeit durch die Proteine SNAP und SNARE und nicht durch Ca $LaTeX: ^{2+}$ vermittelt (s. Kapitel 12). Ca spielt möglicherweise eine Rolle für das Verschließen der Ca-Kanäle bei hohen Ionenkonzentrationen. Die Ca-vermittelte Hysteresis könnte beispielsweise dafür sorgen, dass die Ca- Kanäle geschlossen bleiben, wenn der mittlere Ca-Spiegel nach der elektrischen Erregung wieder auf 10 $LaTeX: ^{-7}$ M abfällt. Wegen der Hysteresis der Entbindung bleiben die Ca-Ionen auch danach noch an der an der Membran lokalisiert, bis die fusionierten Vesikel wieder von der präsynaptischen Membran abgespalten werden.

Aufgabe 10.3:

Differential-Kalorimetrie

Die Messungen thermodynamischer Eigenschaften biologischer Materialien wurden durch die Entwicklung hoch sensitiver Differentialkalorimeter revolutioniert. Die Methode ist prinzipiell extrem einfach, die technische Realisierung dagegen extrem schwierig, da die Methode der Messung des Gewichts einer Fliege auf einem Schiff durch Messung des Gewichts ohne und mit Fliege entspricht. Man kann auch direkt die Wärmezufuhr messen, die notwendig ist, um die Temperatur der beiden Gefäße konstant zu halten.

Das Bild zeigt links oben das Prinzip der Methode. Darunter ist der Temperaturverlauf der Messzellen als Funktion der Zeit dargestellt, wenn man die Temperatur des Wasserbades zeitlich erhöht. Im Fall des Schmelzens der Membran bleibt die Temperatur in der linken Kammer konstant, da dem Gefäß Schmelzwärme entzogen wird. Man kann die Umwandlungswärme direkt messen, wenn man die Wärmekapazität der Messzelle kennt, wie der Text auf der rechten Seite zeigt.

Differntial Kalorimetrie Prinzip

Aufgabe 10.4:

Ein unkonventioneller Ausgangspunkt zur Beantwortung der Frage ist van't Hoff-Gleichung der kooperativen Umwandlung. In diesem Bild des Schmelzvorgangs ist die Schärfe der Phasenumwandlung durch die Zahl N der an der Umwandlung beteiligten Moleküle bestimmt. In diesem Fall bestimmt man den Ordnungsgrad des Materials, der als Bruchteil der umgewandelten Moleküle $LaTeX: \theta$ definiert ist. Nach Gleichung 7.18 ist an der Umwandlungs-Temperatur:

$LaTeX: \frac{d\theta}{dT}=\frac{1}{4}N \frac{\Delta H}{k_BT}$

wobei $LaTeX: \Delta$ H die Umwandlungswärme ist. Daraus folgt, dass die Steilheit der Umwandlung für N $LaTeX: \longrightarrow \infty$ unendlich scharf ist. Wie im Kapitel 7.2.3 gezeigt wurde, kann man die van't Hoff-Gleichung benutzen, um die Zahl der spontan umwandelnden Moleküle zu bestimmen.

In der klassischen Thermodynamik geht man von der Gleichung für die spezifische Wärme $LaTeX: C_p=\frac{d\Delta H}{dT}$ aus, d.h. die spezifische Wärme ist eine $LaTeX: \delta$ -Funktion. Die Umwandlungskurven realer Materialien (wie Kristalle) besitzen stets eine endliche Breite; nicht nur wegen der endlichen Größe, sondern wegen der stets vorhandenen Kristalldefekte wie Versetzungen.

Aufgabe 10.5:

Ordnung der Phasenumwandlung und was wir daraus lernen können

Die formale Ehrenfest'sche Definition der Ordnung der Phasen-Umwandlung lautet:

Bei Phasenumwandlungen erster Ordnung sind die ersten Ableitungen der Freien Energie (F) und freien Enthalpie (G) nach einer thermodynamischen Variablen (T oder p) diskontinuierlich (s. Abb. 9.A). Zwei Beispiel sind:

$LaTeX: S=-[\frac{\partial G}{\partial T}]_p$

$LaTeX: V=-[\frac{\partial G}{\partial p}]_T$

Die S-T- und V-p-Kurven machen bei der Phasenumwandlung einen Sprung (s. Abb. 9.A).

Umwandlungen zweiter Ordnung sind dadurch charakterisiert, dass die ersten Ableitungen stetig sind. Die S-T-Kurven sind s-förmig und haben an der Umwandlung einen Wendepunkt. Daher zeigen die zweiten Ableitungen (z.B. von G) im Bereich der Umwandlung eine scharfe Bande. Dies hat oft die Form eines $LaTeX: \lambda$ und man nennt die Umwandlung daher oft $LaTeX: \lambda$ -Punkt.

Praktisch wichtige Beispiele der zweiten Ableitungen sind:

Die thermische Ausdehnung $LaTeX: \alpha = \frac{1}{V}[\frac{\partial V}{\partial T}]_p$ ;

Die Kompressibilität $LaTeX: \kappa=-\frac{1}{V}[\frac{\partial V}{\partial p}]_S= -\frac{1}{\rho}[\frac{\partial \rho}{\partial p}]_S$

Die Spezifische Wärme $LaTeX: C_p=T [\frac{\partial S}{\partial T}]_p = -[\frac{\partial^2 G}{\partial T^2}]_p$

Wird Helium auf 2.17 $LaTeX: \degree$ K abgekühlt, zeigt die Wärmekapazität eine bemerkenswerte Diskontinuität. Die Dichte der Flüssigkeit nimmt ab und ein Teil des Heliums wird suprafluid, d.h. die Viskosität wird null. Ursache ist die Bose-Kondensation des suprafluiden Teils des Heliums. Der Übergang ist der Prototyp einer Phasenumwandlung zweiter Ordnung.

Phasenumwandlungen

Eine fundamentale Theorie zur Beschreibung von Phasenumwandlungen zweiter Ordnung ist die Landau-Theorie (siehe Webseite). Diese stellt einen Bezug zwischen der rein thermodynamischen Definition der Ordnung einer Umwandlung und den Materialeigenschaften (vor allem der Struktur) her. Zur Charakterisierung des Zustandes führt man den Ordnungsgrad ein. Beispiele sind die Dichte, oder die Orientierung der Moleküle in einer Membran oder Lipid-Monoschicht (s. Aufgabe 9.1).

Es gilt folgende Faustregel: Findet bei der Umwandlung nur eine Änderung der Orientierung der Moleküle statt, so ist diese von zweiter Ordnung. Falls die Umwandlung aber gleichzeitig mit einer Dichteänderung einher, ist sie von erster Ordnung.

Weshalb ist die Frage nach der Umwandlung interessant? Die Landau-Theorie ist sehr hilfreich, um etwas über die strukturelle Änderungen von Materialien bei Phasenumwandlungen von Lipid-Monoschichten oder Membranen zu lernen. Insbesondere liefert die Theorie Messvorschriften zur Messung der Wärmekapazität oder der Thermischen Ausdehnungskoeffizienten. Besonders wichtig ist die Landau-Theorie zur Untersuchung thermischer Fluktuationen. Sie ist auch hilfreich, um etwas über Lipid-Protein-Wechselwirkungen zu lernen.

Aufgabe 10.6:

Modifikation des pH an der Oberfläche geladener Membranen Die Abweichung der Verteilung der Protonen an der Oberfläche von der in der Lösung ist durch die Boltzmann-Verteilung bestimmt.

$LaTeX: \frac{[H^+]_m}{[H^+]_o}=e^{-\frac{e \Phi}{kT}}$

wobei [H] $LaTeX: _{m,o}$ die Konzentrationen an der Oberfläche (m) und in der Lösung (o) sind. Nun gilt folgender Zusammenhang zwischen der Protonenkonzentration und dem pH. pH=- log a oder pH $LaTeX: \approx$ - log [H]. a ist die Aktivität der Wasserstoffionen, die aber in guter Näherung gleich deren Konzentration ist. Es gilt also

$LaTeX: pH_m - pH_0 = \frac{e \Phi}{kT} \approx \frac{100}{25}$

Man beachte noch: $LaTeX: k_BT(300K) \approx 25$ meV. Daher wird die Änderung des pH:

$LaTeX: \Delta pH = 4$

Vergleich mit der Realität: Das Oberflächenpotential lässt sich mit der Gleichung Gl 10.6 berechnen

$LaTeX: \Phi_0=\frac{2k_BT}{e}arcsinh(\frac{0.135 \alpha}{A \sqrt{c}})$

Dabei wird die Fläche pro Lipid in Angström und die Konzentration in $LaTeX: \frac{M}{l}$ eingegeben. Für 300 $LaTeX: \degree$ K ist der Vorfaktor $LaTeX: \frac{2 k_BT}{e}\approx 51.4 mV$ .

Sind alle Lipide einfach geladen ( $LaTeX: \alpha$ =1) so wird für c $LaTeX: \approx 10^{-2}$ ; c $LaTeX: \approx 10^{-3}$ ; c $LaTeX: \approx 10^{-4}$ M: $LaTeX: \Phi_0 \approx$ 1mV; $LaTeX: \Phi_0 \approx$ 3,5 mV; $LaTeX: \Phi_0 \approx$ 10 mV. Wir sehen: Die Änderungen des pH sind unter physiologischen Bedingungen nicht sehr groß.

Aufgabe 10.7:

Bruchteil der gauche-Konformationen. Kinken als treibende Kraft der $LaTeX: H_2O$ -Permeation von Membranen

Vorbemerkung: Die dynamischen Prozesse der Membranen ist durch die Kinetik der Bildung von gauche-Konformationen und gtg-Kinken bestimmt. Man nennt diese thermisch angeregten Konformationen und deren Kombinationen auch Kettendefekte. Die Beweglichkeiten der Kettendefekte bestimmt die dynamischen Eigenschaften der Biomembranen, wie die rotatorische und translatorische Diffusion der Lipide. Sie sorgen aber auch für die Bildung freien Volumens und darüber für die Aufnahme kleiner Moleküle (wie Wasser) und deren Transport in der Membran. Die Untersuchung der Kettendynamik ist daher eine wichtige Aufgabe. Neben spektroskopischen Methoden wie der NMR-und Ramanspektroskopie ist vor allem die Quasielastische Neutronenbeugung (QENS) ein wichtige Methode (s. Aufgabe 10.8).

Berechnung des Bruchteils $LaTeX: \phi_g$ an gauche-Konformationen (s. Kapitel 10.3.1):

$LaTeX: \phi_g=\frac{n_g}{n_g + n_t}$ wobei $LaTeX: n_g$ und $LaTeX: n_t$ die Zahl der $LaTeX: CH_2$ -Gruppen in der gauch- und trans-Konfiguration sind. $LaTeX: \phi_g$ wird durch die Boltzmann-Verteilung bestimmt, unter Berücksichtigung der Anregungsenergie des trans $LaTeX: \longrightarrow$ gauche Übergangs : $LaTeX: \Delta E \approx 4 \frac{kJ}{M}$ . Für 37 $LaTeX: \degree$ C (410 $LaTeX: \degree$ K $LaTeX: \approx 5.65 \frac{kJ}{M}$ , da $LaTeX: k_B=1.38 10^{-23}$ J)) wird:

$LaTeX: \phi_G\approx \frac{n_G}{n_g + n_t} \approx \frac{1}{1+e^{\frac{\Delta \Phi}{k_BT}}}\approx 0.27$

Messungen mittels Raman-Spektroskopie liefern eine Erhöhung von $LaTeX: \phi_g \approx 0.07$ auf $LaTeX: \phi_g \approx 0.4$ .

b) Kinetik der trans-gauch Übergänge: Die Übergangsraten der trans $LaTeX: \longrightarrow$ gauche Übergänge erhält man aus der Arrhenius-Gleichung:

$LaTeX: k_{t\longrightarrow g}=\nu_T e^{\frac{-E*}{RT}}\approx 0.015 \cdot 10^{13} \approx 1.5 \cdot 10^{11} \frac{1}{s}$

Nach Abb. 10.7 ist die Aktivierungsenergie E* $LaTeX: \approx 10 \frac{kJ}{M}$ . Bei 37 $LaTeX: \degree$ C ist RT $LaTeX: \approx 2.4 \frac{kJ}{M}$ . Die Frequenz der Torsionsschwingungen ist $LaTeX: \mu_T \approx 1013$ Hz.

c) Der Diffusionskoeffizient der Bewegung der Kinken durch die Membran folgt aus der Einstein-Beziehung; $LaTeX: D=k_{kink}\frac{\lambda^2}{2}$ , wobei $LaTeX: \lambda$ die Sprungweite der Kinken ist. Nach Abb 10.7c ist diese $LaTeX: \lambda \approx$ 0.13 nm (1.3 A). Nun muss man jedoch noch beachten, dass die Sprungrate nicht $LaTeX: k_{t\longrightarrow g}$ ist. Da man bei jedem Sprung zwei trans-gauche Übergänge anregen muss, ist E* doppelt so groß. Es wird daher:

$LaTeX: k_{kink} \approx n_t e^{-8.33} \approx 10^{13} \cdot 0.00024 \approx 2.4 10^9 \frac{1}{s}$

Man erhält dann für den Diffusionskoeffizienten der Kinken. $LaTeX: D \approx 2.4 \cdot 10^9 \cdot 0.07 10^{-18} \approx 0.15 10^{-9} \frac{m^2}{s}$ .

Kinken

Zusatzfrage: Der Diffusionskoeffizient kann mittels QENS bestimmt werden, wie in Aufgabe 10.8 gezeigt wird.

Die Diffusion der gtg-Kinken entlang der Ketten spielt eine wichtige Rolle als treibende Kraft der Permeation keiner Moleküle (wie Wassermoleküle, Lokalanästhetika) durch die Membran. Die Permabilität des Wassers kann direkt mit der Diffusion der Kinken durch die Membran korreliert werden, wie von Hermann Träuble gezeigt wurde (s. Träuble 1971).

Zur Literatur: Eine sehr gut verständliche Darstellung der durch Kinken angetriebenen Wasser-Permeation: H. Träuble, The movement of Molecules across Lipid-Membranes: A molecular Theory (J Membrane Biol.4, 193-208 1971)

Aufgabe 10.8:

Messung der Diffusion mittels Quasielastischer Neutronenbeugung (QENS).

Wie in Kapitel 10.7 beschrieben wurde, hat die QENS-Technik den Vorteil, dass man sowohl interne Bewegungen einzelner Moleküle (oder Gruppen von Molekülen) als auch kollektive Bewegungsprozesse quantitativ untersuchen kann. Anstatt des aus der quasielastischen Lichtstreuung bekannten dynamischen Strukturfaktor $LaTeX: S(\vec{q},\omega)$ bestimmt man im Experiment meist die sogenannte intermediäre Streufunktion: $LaTeX: S(\vec{q},t)=\int_{-\infty}^\infty d\omega S(\vec{q},\omega)$ und aus dieser den Strukturfaktor durch inverse Fouriertransformation. Die theoretischen Grundlagen wurden in Kapitel 10.7 beschrieben. Die intermediäre Streufunktion und der dynamische Strukturfaktor haben die Form:

$LaTeX: I_{inc}(\vec{q},t)=C \cdot e^{-\vec{q}^2Dt}$ oder $LaTeX: S_{inc}(\vec{q},\omega)= \frac{2C}{\pi}\frac{D\vec{q}^2}{\omega^2+(D\vec{q}^2)^2}$

Der Streuvektor $LaTeX: \vec{q}$ bestimmt die Richtung des Impulsübertrages. Durch Verwendung orientierter Membranen (Lipid-Mutischichten) kann man die Richtung der Impulsübertragung und der Molekülbewegung festlegen. Um die Diffusion in der Ebene der Membran zu messen muß $LaTeX: \vec{q}$ parallel zur Membranebene orientiert sein (s. Abb 9.8a). Das rechte Bild zeigt die Orientierung $LaTeX: \theta$ =135 Grad die Diffusion in der Ebene gemessen wird.

Abb 9.8A. Rechts: Orientierung der Lipid-Multischichten zur Messung der Impulsübertragung parallel ( $LaTeX: \vec{q}_{\parallel})$ und senkrecht ( $LaTeX: \vec{q}_\perp)$ zur Membrannormalen $LaTeX: \vec{n}$ . Links: Drei gemessene Strukturfaktoren. Man beachte die Verbreiterung der Linie beim Übergang von $LaTeX: \theta$ = 15 bis $LaTeX: \theta$ = 120 Grad. Die Abszisse wird üblicherweise in meV angegeben, wobei 1meV $LaTeX: \approx 0.24 10^{12}$ Hz.

Zusatzfrage: Protonen haben den Kernspin I= $LaTeX: \frac{1}{2}$ und Deuteronen I=1. Während der (Fermi Kontakt-) Wechselwirkung der Neutronen mit dem Spin $LaTeX: \frac{1}{2}$ kann ein zufälliger Spinaustausch stattfinden. Durch diesen verliert das Neutron sein Phasengedächtnis und kann nicht mehr mit dem Primärstrahl interferieren. Die Phasenbeziehung der von benachbarten Positionen des Materials ausgehenden Elementarwellen (d.h. deren Kohärenz) geht verloren. Die Situation ist ganz ähnlich wie bei der Spin-Spin-Relaxation der NMR-Spektroskopie. Der in Resonanz beobachtete Kernspin kann mit Kernen der Umgebung den Spin austauschen und trägt daher nicht mehr zum beobachteten Spektrum bei. Dessen Amplitude fällt exponentiell mit der Zeit ab. Die Relaxationszeit heißt Spin-Spin- oder T2-Relaxationszeit.

Ergänzung: Das rechte Bild der Abb. 9.8a zeigt, dass der QENS-Strukturfaktor (oder die intermediäre Streufunktion) einem elastischen und einem inelastischen Anteil bestehen.

$LaTeX: S(\vec{q},\omega)=S_{ela}(\vec{q})\delta (\omega) + S_{inel}(\vec{q},t)$

Der elastische Anteil $LaTeX: S_{ela}(\vec{q},\omega)$ liefert Information über die statische Struktur des Materials. Misst man diesen als Funktion von q so kann man herausfinden, ob ein Molekül frei beweglich ist ( $LaTeX: S_{ela}(\vec{q}) \longrightarrow 0$ , für $LaTeX: q \longrightarrow \infty$ ) oder nur lokale Zitterbewegungen ausführen kann. Im letzteren Fall erhält man aus dem asymptotischen Wert von $LaTeX: S_{ela}(\vec{q})$ die Amplituden der Auslenkungen. Auf diese Weise kann man die lokale Diffusion der Lipide und die weitreichende Brown'sche Bewegung separat messen.

Ein weiterer Vorteil: Da die Deuteronen bevorzugt kohärent und die Protonen inkohärent streuen, kann man sogar die Bewegung einzelner Molekülgruppen in einem Molekül durch Messung der inkohärenten Streuung bestimmen, indem man den Rest des Moleküls der Protonen durch Deuteronen ersetzt. Der gravierende Nachteil der Neutronenbeugung ist die kleine Empfindlichkeit, weshalb sie vor nur auf Lipid-Multischichten anwendbar ist.

Literatur: (siehe Liste in Kapitel 12).

Aufgabe 10.9:

Zur Poisson-Statistik der Teilchenfluktuation

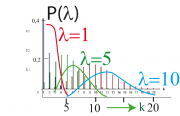
Vorbemerkung Vergleich Gauss- und Poisson-Verteilung: Die Poisson-Verteilung ist wie die Binominalverteilung eine diskrete Wahrscheinlichkeitsverteilung. Sie gibt an, wie oft Ereignisse beim Durchführen eines Zufallexperiments (wie das Werfen einer Münze) auftreten. Die Poissonverteilung ist eine gute Näherung wenn die Wahrscheinlichkeit eines Ereignisses sehr klein ist. Ein Beispiel ist die spontane Öffnung eines Ionenkanals in Nervenmembranen (s. Kapitel 15.7).Ist die Wahrscheinlichkeit eines Ereignisses etwa $LaTeX: \frac{1}{2}$ , so muss man mit der Bernouilli-Verteilung arbeiten. Die Poissonverteilung wird durch den Parameter l bestimmt, der gleich dem Mittelwert der Verteilung ist.

 (10. 9.1)

Drei Beispiele:

Poissonverteilungen

Die Poisson-Verteilung liefert also Voraussagen über die Anzahl (k) des Eintretens seltener, statistischer Ereignisse innerhalb eines bestimmten Intervalls, wenn man den Mittelwert kennt, was oft durch Messung möglich ist (s. Aufgabe Katz-Experiment).

Betrachten wir ein Beispiel.

Besonders einfach sind der Erwartungswert und die Varianz der Ereignisse (s. Wikipedia Stichwort Poissonverteilung):

$LaTeX: E(x)= \sum_0^\infty k \frac{\lambda^k}{k!}e^{-\lambda k}=\lambda$ und $LaTeX: Var(x)=\sum_0^\infty (k-\lambda)^2 \frac{\lambda^k}{k!}e^{-\lambda} \approx \lambda$

Eine Ableitung der Poissonverteilung aus der Binominalverteilung findet man in Wikipedia Stichwort 'Poissonverteilung'.

Beziehung zur Normalverteilung:

Für große $LaTeX: \lambda$ kann die Poisson-Verteilung durch die Gaußsche Verteilung ersetzt werden:

$LaTeX: P(k)\approx \frac{1}{\sqrt{2\pi\lambda}}e^{-\frac{(k-\lambda)^2}{2\lambda}}$ (10.9.3)

Man beachte. Die Poissonverteilung kann durch eine glockenförmige Kurve ersetzt werden falls $LaTeX: \lambda \geq 30$ . Der Erwartungswert wird wie erwartet E(x)= $LaTeX: \lambda$ und die Varianz Var(x) = $LaTeX: \lambda$ .

Die Schwankung der Teilchenzahl: Zur Berechnung der relativen Schwankung der Teilchenzahl $LaTeX: \frac{\delta N}{N}$ in einem Volumen mit N Molekülen gehen wir von der Näherung für große N aus. Anwendung von Gl 10.2.3 liefert:

$LaTeX: Var(n)=<(n-N)^2>= \frac{1}{\sqrt{2\pi N}} \int _{-\infty}^{\infty}dn (n-N)^2 e^{-\frac{(k-N)^2}{2N}}=N$

Die relative Schwankung ist $LaTeX: \frac{\sqrt{n-N}}{N}=\frac{1}{\sqrt{N}}$ Die Teilchenzahl schwankt um einen Faktor 2 falls N=4 ist.

Nachtrag: Eine klassisches Beispiel einer Poissonverteilung trat bei de preußischen Kavallerie auf; Mit der Frage wie oft ein Offizier durch den Tritt eines Pferdes getötet wird. Das sind seltene Ereignisse, da in manchen Jahren kein und in anderen 3 oder gar 5 Offiziere getötet wurden, d.h. die Wahrscheinlichkeit ist p<<1. Da die Zahl N der Offiziere groß war, handelt sich um ein gutes Beispiel der Anwendung einer Poissonverteilung, da man nur den über Jahre bestimmten Erwartungswert $LaTeX: \lambda$ messen musste. In diesem Fall ist die statistische Variable k. Die Wahrscheinlichkeit, dass drei Offiziere getötet werden ist also: $LaTeX: \frac{\lambda^3}{3!}e^{-\lambda}$ .

Aufgabe 10.10:

Fluoreszenz-Korrelationsspektroskopie, Effekt chemischer Reaktionen

Skizierung Ableitung der Fluoreszenz-Korrelationsfunktion für reine Diffusion.

Die Fluktuation des Signals im Detektor ist nach der Gl 10.28:

$LaTeX: I(t)= \int \int \int d^3 r F(r) \sum_i a_i \delta(\vec{r}-\vec{R_i})_R$ (9A1)

Dabei ist F(r) eine Filterfunktion, die angibt, welcher Bruchteil des gesamten emittierten Lichts am Detektor ankommt und registriert wird. Sie ist durch mehrere Faktoren bestimmt und wird in der Regel empirisch bestimmt. $LaTeX: a_i$ ist die Amplitude der emittierten Elementarwellen. Wir berücksichtigen im Folgenden nur die optische Transferfunktion des Objektives. Die Korrelationsfunktion der Fluktuation der Fluoreszenzintensität ist die Funktion i(r,t) = I(r,t)-. Man sollte auch daran denken, dass die Fouriertransformierte der Konvolution zweier Funktion (F(r) und F(r')) das Produkt der Transformationen der Einzelfunktionen sind.

Die Korrelationsfunktion der Intensität hat dann die Form:

$LaTeX: K(\tau)= \frac{\rho}{(2\pi)^6} \int \int \int dV \int \int \int dV' F(r)F'(r) \sum_i a_i \delta(\vec{r}-\vec{R_i}) \sum_j a_j \delta(\vec{r}-\vec{R_j})$

$LaTeX: \rho$ ist die mittlerer Teilchen-Dichte. Mit der Definition der $LaTeX: \delta$ -Funktion

$LaTeX: \delta(\vec{r}-\vec{R_i})=\int _{-\infty ^\infty e^{iq(\vec{r}-\vec{R_i})}}$

folgt schließlich (siehe auch Ableitung des Abbe-Theorems in Kapitel 37):

$LaTeX: K_F(\tau)= \frac{\rho}{(2\pi)^6} \int \int \int d^2\vec{q} F(\vec{q})F'(-\vec{q}) \sum_i \sum_j a_i a_j e^{-i \vec{q}(\vec{R_i}(t)-\vec{R_j}(0))} \propto \int d\vec{q} F(\vec{q})F(-\vec{q})I_{inc}(\vec{q},\tau)$ (9A.2)

Diese Gleichung folgt aus 10.19b, wenn wir noch die Amplituden $LaTeX: a_i$ der Elementarwellen einführen.

Wir nehmen nun als einfachsten Fall an, dass die Verteilung der in den Detektor emittierten Lichts durch die Apertur des Mikroskopobjektivs bestimmt ist und dass dies eine Gaußfunktion ist:

$LaTeX: F(r)= F_0 e^{-\frac{2r^2}{w^2}}$ (9.A3) wobei w der Durchmesser der Objektiv-Apertur ist. Als weitere Vereinfachung nehmen wir an, dass das Volumen aus dem Licht als eine Scheibe registriert wird, d.h. wir vernachlässigen zunächst die zylinderförmige Struktur.

Zur Berechnung der Korrelationsfunktion $LaTeX: K_F(t)$ für reine Diffusion: In Kapitel 10 haben wir die intermediäre Streufunktion ( $LaTeX: I_{inc}(q,t)$ ) und den dynamischen Strukturfaktor abgeleitet (Gl 10.27) und gezeigt, dass für die freie Diffusion folgt:

$LaTeX: I_{inc}(\vec{q},t)=C e^{-\vec{q}^2 Dt}$

Die Berechnung des Produkts der F(q)F(-q) erfolgt über das Konvolutionstheorem. Sie ist einfach, erfordert aber einen gewissen Rechenaufwand. Man beachte dabei, dass die Fourier-Transformierte einer Gaussfunktion wieder eine solche ist, dass die Varianz im Zähler erscheint und dass die Normierung verloren geht.

$LaTeX: \int _{-\infty} ^\infty a e^{\frac{(x-b)^2}{2\sigma^2}}dx = a\sqrt{2\pi} \sigma$

In unserem Fall ist $LaTeX: \frac{1}{2 \sigma^2}= -\frac{w^2}{4} + D\tau$

Daher wird für ein eindimensionale Integration:

$LaTeX: \int _{-\infty} ^\infty e^{q^2 {-\frac{w^2}{4}+D\tau}}= \sqrt{2 \pi}\sqrt{-\frac{w^2}{4}+D\tau}$

Da wir in unserem Fall der zweidimensionalen Scheibe berücksichtigen müssen, dass $LaTeX: \vec{q}=(q_x,q_y)$ ist, folgt:

$LaTeX: K_F (\tau) = const \frac{1}{1+\frac{4D\tau}{w^2}}$ (9.A4)

Wir betrachten nun den Fall, dass die molekularen Sonden gleichzeitig an einer chemischen Reaktion teilnehmen können, bei der die Fluoreszenz verloren geht oder das Molekül mit einer anderen Farbe leuchtet. Wir betrachten die Reaktion M + A $LaTeX: \longrightarrow$ M* . Die Bindungskonstante sei K und die Raten der Hin- und Rückreaktion seien $LaTeX: k_1$ und $LaTeX: k_2$ , mit $LaTeX: K=\frac{k_1}{k_2}= \frac{am}{m*}$ , wobei kleine Buchstaben für die Konzentrationen stehen. Der Bruchteil der Moleküle im Zustand M* wird: $LaTeX: m*= \frac{1}{1+K'}$ . Wir müssen nun das zeitliche Verhalten des Zustandes M betrachten. Die Ratengleichung lautet:

$LaTeX: \frac{dM*}{dt}=k_1ma-k_2m*$

Die Lösung der Gleichung hat die Form $LaTeX: M*=M(0)e^{\frac{t}{t_g}}$ . Es folgt schließlich:

$LaTeX: K_F(\tau) \propto \frac{1-m*}{N}(1+\frac{1}{1-m*}e^{\frac{\tau}{t_R}}(\frac{1}{1+\frac{4D\tau}{w^2}})$ (9.8.5)

Wir haben bei der Ableitung die zylindrische Form des Beobachtungsvolumen vernachlässigt und ein 2D- Volumen angenommen. Durch die zylindrische Form wird noch ein Korrekturfaktor der Form $LaTeX: \frac{1}{1+\frac{\tau}{S^2D}}$ eingeführt(siehe. Rusu et al Biophys. J. 87 1044-1053 (2004)). Dabei ist S das Verhältnis des Durchmessers zur Länge des zylinderförmigen Fokus.

Zur Literatur: Wir haben bei der Ableitung der Korrelationsfunktion der Intensitätsfluktuation die Methode von J. Rica und T. Binkert (Phys. Rev.A 39, 2646 (1989)) benutzt, da sie von der fundamentalen Idee ausgeht, die Dichteverteilung der Sonden oder Moleküle zur Untersuchung der Struktur und Dynamik der Materie auszunutzen. Dadurch wird die lehrreiche Analogie zwischen der inkohärenten Neutronenbeugung und der FCS klar. Eine andere, mehr konventionelle Ableitung findet man in Hess et al. Biochemistry. 41:697 - 705.(2002).

Search

Navigation

SEARCH

TOOLBOX

LANGUAGES