Lösungen Kapitel 11

From BioPhy.de Wiki

Aufgabe 11.1:

Wie bei der Behandlung der Erythrozytenformen erwähnt, ist zur Beschreibung der Deformation weicher Materialien häufig vorteilhaft, die vereinfachte Version der Elastizitätstheorie von Moony und Rively zu verwenden. Diese wurde zur Beschreibung von sehr stark dehnbaren weichen Materialien entwickelt. Die konventionelle lineare Theorie gilt für sehr kleine Deformationen der Festkörper, deren Elastizitätsgrenze (yield strain) bei Deformationen von 0.2% liegt. Weiche Materialien lassen sich oft um 50% dehnen und die lineare Theorie der Elastizität gilt nicht mehr. Eine umfassende Darstellung findet man in Wikipedia; Stichwort 'Mooney-Rivlin solid'.

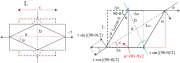
Zur Diskussion betrachten wir ein Quadrat der Seitenlänge L, das von zwei Paaren von Normalspannungen $LaTeX: \tau_1$ und $LaTeX: \tau_2$ zu einem Rechteck deformiert wird- (s. Abb. 10A.1) Wie in Kapitel 11 beschrieben, definieren wir als Dehnung (strain) die normierte Verlängerung $LaTeX: \lambda_i = \frac{L_i}{L}$ in der Richtung i (s. Abb 10.A1):

Visualisierung von Deformation

Wir betrachten hier nur reine Scherungen. Wie im Kapitel 11 gezeigt, wurde gilt für diesen Fall:

$LaTeX: \lambda_\chi = \frac{L_\chi}{L}$ und $LaTeX: \lambda_2 = \lambda ^{-1}$

Wie außerdem in Wikipedia gezeigt wird, ist das elastische Gleichgewicht durch folgende Gleichung bestimmt:

$LaTeX: \sigma_{\chi \chi}- \sigma_{zz}= 2\tau = \mu (\lambda^2-\lambda^{-2})=\mu(a^2 - b^2)$

wobei a und b der lange und kurze Durchmesser der Raute sind. Wir können die Streckung $LaTeX: a^2- b^2$ auch für die konventionelle Definition der Scherung berechen; Aus dem rechten Bild erhalten wir mit $LaTeX: tan(\theta)=\frac{\sigma}{\mu}$ :

$LaTeX: a^2 = L^2 [1+(1+\frac{\Delta x}{L})] = L^2 [1+(1+tan(\theta))^2]$ und $LaTeX: a^2 -b^2 =4tan(\theta)=4 \frac{\sigma}{\mu}$

Aufgabe 11.2:

Da nur wenige Probleme der Elastizitätstheorie analytische lösbar sind (die meisten findet man in Landau und Lifshitz Vol VII 'Elastizitätstheorie') ist es sehr wichtig zur Abschätzung von Effekten Näherungen der Deformationen zu benutzen. Da elastische Deformationen meist klein sind, liefert das Verfahren schon gute Ergebnisse.

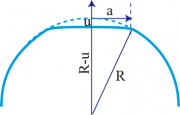
Für den betrachteten Fall der Kugelkappe findet man die die Zusammenhänge zwischen der Deformation u (Kappendicke), dem Radius R der Kugel und dem Radius a der Basis der Kugelkappe in der Formelsammlung von Bronstein und Semendiajew.

Kappendeformation

a: Kappenradius R: Radius u: Kappentiefe

$LaTeX: a^2+(R-u)^2=R^2$ $LaTeX: a^2=2Ru-u^2$ $LaTeX: a=\sqrt{2Ru-u^2}$

a) Die erste Ableitung ist $LaTeX: \frac{du}{dx}\approx \frac{u}{R}$ . Die dadurch induzierte Spannung in der Kappe: $LaTeX: \sigma = Eh \frac{u}{R}$ , wobei Eh der zweidimensionale E-Modul der Schale der Dicke d ist. Die Dehnungsenergie (pro Fläche) wird dann $LaTeX: E_{Dehnung} \approx Eh \frac{u}{R}$ .

Die zweite Ableitung ist von der Größenordnung $LaTeX: \frac{d^2 u}{dx^2} = \frac{d}{dx} \frac{du}{dx} \approx \frac{u}{R^2}$

Die Biegeenergie der Deformation ist Biegemodul [ $LaTeX: \kappa$ mal $LaTeX: (\frac{d^2u }{dx^2})^2$ )]: $LaTeX: E_{Biegung}\approx Eh^3 (\frac{u}{R^2})$

Man beachte den wichtigen Unterschied zwischen schwach gebogenen Platten und kleinen Deformationen der Kugelschale. Das Verhältnis Dehnungsenergie zu Biegeenergie ist im Fall der Kugelschale von der Größenordnung $LaTeX: (\frac{R}{u})^2$ , während die Dehnung im Fall der Platten vernachlässigbar ist, falls u<<h. Die Situation ändert sich, falls die Kugel Überschussfläche hat oder ein Loch, da dann die Dehnung wieder ein Effekt zweiter Ordnung ist.

b) Der Unterschied zwischen Platte und Schale wird besonders beim Lösen der zweiten Aufgabe einsichtig:

$LaTeX: R \rightarrow R + \zeta$ $LaTeX: U = 2 \pi (R+ \zeta) \rightarrow \Delta U = 2\pi \zeta$

Die relative Dehnung ist: $LaTeX: \frac{u}{R}$ . Für $LaTeX: R \rightarrow \infty$ , d.h. für eine Platte geht die relative Dehnung gegen null. Eine alte Scherzfrage lautet: Um die Erde zu stabilisieren, schmiedet Atlas einen Ring um den Äquator. Er macht ihn aber einen Meter zu lang. Wie weit steht der Ring von der Oberfläche ab?

Die Änderung des Umfangs ist $LaTeX: \Delta U=2 \pi \zeta$ . Daher wird $LaTeX: \zeta = \Delta U/ 2 \pi = \frac{1m}{2 \pi} \approx 16$ cm, was auf den ersten Blick überraschend ist. Die relative Dehnung ist aber wieder sehr gering:

$LaTeX: \frac{\Delta U}{U}=\frac{\zeta}{R}\approx 2.35 \cdot 10^{-8}$

Aufgabe 11.3:

In Kapitel II haben wir gesehen, dass die Formenvielfalt der Riesenvesikel aus einer Lipidkomponenten schon sehr reich ist und durch drei Parameter bestimmt wird: Das Flächen-zu-Volumen Verhältnis und die spontane Krümmung $LaTeX: C_0$ . Bei nur einer Komponenten sind die Doppelschichten symmetrisch und im thermodynamischen Gleichgewicht ist $LaTeX: C_0= 0$ . Bei der spontanen Bildung der Vesikel aus Multischichten (durch Quellen in Wasser) haben die beiden Monoschichten zunächst dieselbe Fläche $LaTeX: A_0$ , so dass nach der Bildung der Vesikel der innere Monofilm lateral etwas komprimiert und der äußere expandiert werden muß. 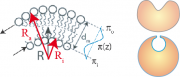Der Radius des Vesikels sei R und die Fläche der 'neutralen Fläche' (die im Fall symmetrischer Membranen zwischen den Monoschichten liegt) ist $LaTeX: A_0=4 \pi R_0^2$ . Die Flächen der äußeren ( $LaTeX: A_a$ ) und inneren Monoschicht ( $LaTeX: A_a$ ) sind dann (s. Abb.9.A1):

$LaTeX: A_a = 4 \pi (R_0 + \frac{d_m}{2})^2$ und $LaTeX: 4\pi (R_0 - \frac{d_m}{2})^2$

Die relative Flächendifferenz im Vesikel ist daher $LaTeX: \Delta A =(A_a - A_i)^2 \approx 8\pi R_0^2 \frac{d_m}{R_0}=2A_0\frac{d_m}{R_0}$

Zwei Formen von Vesikeln minimaler elastischer Energhie, die aus einer Platte aus einer Doppelschicht mit gleichen Monofilmflächen entstehen können

Nach Gl. 11.37 ist die Biegeenergie, die zur Bildung der geschlossenen Schale aus der flachen Scheibe notwendig ist:

$LaTeX: G_{curv}^{global}= \frac{1}{2} \kappa ' \frac{\pi}{A d_m^2}(\Delta A - \Delta A_0)^2$ (11. 7)

da $LaTeX: \Delta A_0=0$ ist. Diese Energiekosten werden durch Bildung von Stomatozyten-Formen oder nach innen zeigende Knospen reduziert. Da der Ausgangszustand nicht bekannt ist, kann man die entstehende Form nicht vorhersagen.

b) Die Vesikel können durch Transfer von Lipiden von der inneren zur äußeren Monoschicht(oft Lipid-flip-flop genannt) in quasisphärische Vesikel übergehen. Dieser Übergang kann in reinen Lipidmembranen sehr langsam (d.h. mit Halbwertszeiten von \char`\~ 10h) erfolgen.

Zusatzinformation zur Beobachtung der Kinetik des Lipid-flip-flops.

Eine elegante Methode zur Messung der Kinetik des flip-flops ist die Differential-Kalorimetrie (T. Bayerl et al. Biochemistry 27, 6078 (1988))

Man kann den Transfer zwischen Vesikeln aus verschiedenen Lipiden wie DMPC und DPPC bestimmen, oder aus gleichen Lipiden wie DMPC. Dazu verwendet man Lipide mit deuterierten Ketten, wie DMPC-d54.

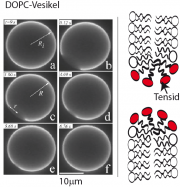
Die folgende Abbildung zeigt ein experimentelles Ergebnis für DMPC und DMPC-d54 Vesikel. Die detaillierte Analyse der Kinetik des Transfers wird in [Bayerl et al] beschrieben. Dort wir auch gezeigt, wie man zwischen dem Austausch der Lipide zwischen den Vesikeln und dem flip-flop zwischen den Monoschichten unterscheiden kann.

Die Halbwertszeit des flip-flops (ff) hängt vom Phasenzustand der Lipide und vor allem von der Kettenlänge ab. Die Halbwertszeit für DMPC bei 35 \degree C ( $LaTeX: T>T_m$ ) ist 5h und für DPPC bei 35 \degree C (d.h. $LaTeX: T<T_m$ ) 46 h.

Rechts: Thermogramme einer Suspension aus Vesikeln aus DMPC und DMPC-d54 die zu den angegebenen Zeiten nach der Herstellung beobachtet wurden. Man erkennt, daß die beiden Banden langsam verschmelzen: Nach 24 Stunden sind die Lipide vollständig ausgetauscht. Links: Die aus der Analyse der Thermogramme bestimmten Kinetiken des Austausches. Unten Beobachtung des Übxergangs von DMPC zu DMPC d54. Oben: Kinetik des umgekehrten Transfers.

Aufgabe 11.4:

Ausgangspunkt ist der Zusammenhang zwischen dem Young-Modul E, der Schalendicke h und der (in der Regel unbekannten) Poissonzahl $LaTeX: \nu$ (s. Gleichung 11.6a):

$LaTeX: \kappa = \frac{Ed_m^3}{12(1-\nu^2)}=\frac{1}{9}Ed_m^3$ für $LaTeX: \nu=\frac{1}{2}$ .

Mit $LaTeX: E=10^{12} Pa$ wird $LaTeX: d_m = \sqrt[3]{\frac{9 \kappa}{E_{Gold}}}\approx 2.5 A$ .

Aufgabe 11.5:

Ausbeulung

Bei Vernachlässigung von Randeffekten wird für Ausbeulungen, die bezüglich der z-Achse rotationssymmetrisch sind ( $LaTeX: R_x= R_y$ ) der Zusatzdruck:

$LaTeX: p=\frac{2\sigma}{R}$

Man beachte, dass in fluiden Membranen die laterale Spannung stets isotrop ist und die Ausbeulungen rotationssymmetrisch sind. Membranen, die durch Vernetzung der Komponenten Schersteifigkeit besitzen, können anisotrope Ausbeulungen besitzen, die durch zwei Krümmungsradien $LaTeX: R_x$ und $LaTeX: R_y$ bestimmt sind. In diesem Fall lautet die Laplace-Gleichung:

$LaTeX: p=\sigma (\frac{1}{R_x}+ \frac{1}{R_y})$

Zusatzfrage; Für $LaTeX: R_x$ 100 nm und $LaTeX: \sigma =10^{-1} \frac{N}{m}$ wird $LaTeX: p \approx 2 \cdot 10^3 \frac{N}{m^2}$ . Man beachte: Der Wert von $LaTeX: \sigma= 10^{-4} \frac{N}{m}$ entspricht etwa 10 \

Aufgabe 11.6:

a)Da Lernziel dieser Aufgabe ist die Kenntnisse der Fourierzerlegung aufzufrischen.

Man betrachtet eine ebene Membran der Dimension L $LaTeX: \cdot$ L. Die Biegeenergie ist:

$LaTeX: G_{ela}=\frac{1}{2}\int \int dO [\kappa (\Delta u(x,y))^2 + \sigma (\nabla u(x,y))^2]$ (11.6,1)

Es ist zu beweisen:

$LaTeX: G_{ela}=\frac{L^2}{2} [\sum_{q_{min}}^{q_{max}} u_q^2[\kappa q^4 + \sigma q^2]]$

Dabei ist $LaTeX: q_{min}= \frac{\pi}{h}$ und $LaTeX: q_{min}= \frac{\pi}{L}$ , wobei h die Membrandicke ist.

Allgemeine 2D Fourierzerlegung:

$LaTeX: u(x,y)= \frac{1}{(2\pi)^2} \sum_{-\frac{\pi}{L}}^{\frac{\pi}{L}} \sum_{-\frac{\pi}{L}}^{\frac{\pi}{L}} (u(q_x,q_y) e^{-2 \pi i (q_xx+q_yy)})$ $LaTeX: G_{ela}^{Biegung}=\frac{1}{2}\frac{1}{(2\pi)^2}\int \int dx dy \sum_{-\frac{\pi}{L}}^{\frac{\pi}{L}} {\kappa((4\pi)^2u(q_x,q_y)^4(q_x^2 + q_y^2)^2})$

Wir betrachten nur den ersten Teil des Energiefunktionals (d .h. die Biegeenergie). Da die Beträge der Exponentialfunktionen eingehen, können wir für quadratische Membranplatten (wegen $LaTeX: q_x=q_y =q$ ) schreiben:

$LaTeX: G_{ela}^{Biegung} = \frac{\kappa}{2} \sum_{-\frac{\pi}{L}}^{\frac{\pi}{L}} q^2 u^2$

Auf dieselbe kann man den Beitrag der Spannung berechnen und die Gleichung beweisen.

b) Der Übergang vom dem durch die Biegeenergie dominierten zu dem spannungsdominierten Verhalten erfolgt bei:

$LaTeX: q=\sqrt{\frac{\sigma}{\kappa}}$

Die Länge $LaTeX: \lambda_c=\pi \frac{\kappa}{\lambda}$ heißt Kapillarlänge, deren Bedeutung bei der Adhäsion der Vesikel ausführlich diskutiert wird.

Zusatzfrage zu Eigenfunktionen der geschlossenen Vesikel:

Die Behandlung ist sehr viel komplizierter, da man sphärisch harmonische Funktionen als Eigenfunktionen der thermischen Anregung der Vesikel einsetzen muss. Eine ausführliche Berechnung findet man in Schneider et al: J Physique 45 1457 (1984).

Die Anwendung zur Messung der Biegesteifigkeiten der Vesikel durch Fourieranalyse der Vesikel wird ausführlich beschrieben in: Engelhardt et al., J Physique Letters 46 L395-L400, (1985). Dort wird auch gezeigt, dass man die Fourieramplituden allein durch Fouirieranalyse der Kontur der Vesikel bestimmen kann.

Eine Beschreibung der Analyse der Eigenschwingungen (Modenanlyse) quasisphärischer Vesikel mit Exzessfläche aus der oben angegebenen Arbeit von Häckl et al J de Physique.

Modenanalyse

Search

Navigation

SEARCH

TOOLBOX

LANGUAGES