Lösungen Kapitel 12

From BioPhy.de Wiki

Aufgabe 12.1:

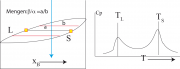
Man kann die Aufgabe graphisch lösen (wie in Abb. 12A), indem man die Kurven der freien Energie der binären Mischungen in der festen ( $LaTeX: \Delta G^{\beta}$ ) und fluiden Phase ( $LaTeX: \Delta G^\alpha$ ) für verschiedene Temperaturen berechnet und als Funktion des Molenbruchs einer Komponente (meist $LaTeX: x_B \equiv 1-x$ ) aufträgt. Wir beschreiben beide Wege.

Erinnerung an Definitionen und Daten für DMPC und DPPC: Partielle molare Größen (engl. partial molar quantities) sind die Ableitungen der exzessiven thermodynamischen Größen (Thermodynamische Potentiale, Druck, Volumen Entropie) nach der Molzahl $LaTeX: n_i$ . Insbesondere ist das chemische Potential $LaTeX: \mu_i = \frac{\partial G}{\partial n_i}|_{p,n_i}$ . Umwandlungswärme ( $LaTeX: \Delta H_m$ , engl. standard enthalpy of fusion) und thermische Energie, die aufgewendet werden muss, um ein Mol der Lipide zu schmelzen.

Tabelle für DMPC & DPPC:

Umwandlungstemperaturen $LaTeX: T_m$ : & $LaTeX: T_m$ = 296 ° K & $LaTeX: T_m$ =313 ° K

Umwandlungswärmen $LaTeX: \Delta H_m$ : & $LaTeX: \Delta H_m = 25 \frac{kJ}{M}$ & $LaTeX: \Delta H_m = 38 \frac{kJ}{M}$

Umwandlungsentropien $LaTeX: \Delta S_m$ : & $LaTeX: \Delta S_m = 84 \frac{J}{MK}$ & $LaTeX: \Delta S_m = 120 \frac{J}{MK}$

$LaTeX: \Delta S_m=\frac{\Delta H_m}{T_m}$

Ausgangspunkt für die graphische und analytische Bestimmung der Phasendiagramme ist die gesamte Änderung der freien Energie:

$LaTeX: \Delta G= x_A \Delta G_A^0 + (1-x_A)\Delta G_B^0+ \Delta G_m$ (12.11)

Dabei ist $LaTeX: \Delta G_A^0= -(G_A^\beta -G_A^\alpha)$ der Unterschied der freien Energie der Komponente A zwischen der festen und in der fluiden Phase. Analog gilt für die Komponente B: $LaTeX: \Delta G_B^0= -(G_B^\beta -G_B^\alpha)$ . Die Wahl der Vorzeichen ist (wie in Abb. 12A) dadurch bestimmt, dass wir als Standardzustand die Mischung aus den fluiden Phase der Komponenten A und B nehmen und uns zwischen den Schmelztemperaturen der beiden Komponenten befinden. Wir betrachten der Einfachheit halber auch nur den Fall idealer Mischungen, für die der Beitrag der Mischungsentropie folgende einfache Form hat:

$LaTeX: G_{m,i}= RT {x_i ln x_i +(1-x_i) ln(1-x_i)}$ (12.1.2)

Weg 1. Graphische Lösung: Bei der Auftragung der freien Energie muss man noch Folgendes beachten. Erstens: Der Unterschied der Schnittpunkte der Parabel mit der Ordinate bei $LaTeX: x_A=0$ bzw. $LaTeX: x_A=1$ gegeben ist durch $LaTeX: \Delta G_A^0= -(G_A^\beta -G_A^\alpha)$ bzw. $LaTeX: \Delta G_B^0= -(G_B^\beta -G_B^\alpha)$ . Zweitens: Die in Abb. 12.1.1 wiedergegebenen Parabeln verschieben sich bei Annäherung an die Umwandlungstemperatur mit zunehmender Temperatur nach oben.

In der linken Abbildung sind die Parabeln der freien Energien für eine Situation eingezeichnet, in der die Mischung in eine A-reiche fluide $LaTeX: L_\beta$ -Phase und eine B-reiche $LaTeX: L_\beta$ -Phase zerfällt. Man befindet sich oberhalb der Umwandlung der Komponente A. Rechts von der Zusammensetzung a ist man im fluiden, links von b in der festen Phase und dazwischen findet der Zerfall in die beiden Phasen statt. Im mittleren Bild wurde die Temperatur erhöht. Dabei wandert vor allem das Minimum der Parabel der fluiden Mischung ( $LaTeX: L_\alpha$ ) nach rechts. Im rechten Bild werden drei Situationen gezeigt, in denen man sich (von oben nach unten) weit oberhalb der Liquiduslinie, an der Temperatur der derselben und weit unterhalb der Soliduslinie befindet.

Zur graphischen Bestimmung der Phasengrenzen

Weg 2: Analytische Berechnung des Phasendiagramms: Man geht von Gleichungen 12.A.1 für die freie Enthalpie der Molekülsorten A und B aus.

Im Phasengleichgleichgewicht (d.h. an den zwei Phasengrenzen) sind die chemischen Potentiale jeder Komponente in den beiden Phasen gleich. Wir betrachten die Komponente A.

Da das chemischen Potential ( $LaTeX: \mu_A$ ) ein Maß für die Arbeit ist, ein Molekül A vom Zustand niedriger in den Zustand höherer freier Enthalpie zu verschieben, brauchen wir nur die Änderung der Molzahl dieser Komponente von $LaTeX: N_A$ zu betrachten. Wir müssen aber dann berücksichtigen, dass in jeder Phase gilt:

$LaTeX: x_A^{\alpha(\beta)} + x_B^{\alpha(\beta)} = 1$ (12.1.3)

Da wir für die Berechnung der chemischen Potentiale nur die Variation einer Komponente (A oder B) betrachten müssen, folgt:

$LaTeX: N (\mu_A^\alpha - \mu_A^\beta)=\Delta G_A^0+RTln(\frac{x_A^\alpha}{x_A^\beta})$ (12.1.4)

Eine analoge Gleichung erhält man für die Komponente B. Man erhält daher das folgende Gleichungssystem:

$LaTeX: \frac{x_A^\alpha}{x_A^\beta} = e^{-\frac{\Delta G_A^0}{RT}}$ und $LaTeX: \frac{x_B^\alpha}{x_B^\beta} = e^{\frac{-\Delta G_B^0}{RT}}$ (12.14)

Man kann nun mit Hilfe der Bedingung (b) in der linken Gleichung einmal $LaTeX: x_A^\beta$ und einmal $LaTeX: x_A^\alpha$ eliminieren und erhält:

$LaTeX: x_A^\beta=\frac{e^{\frac{-\Delta G_A^0}{RT}} [1-e^{-\frac{\Delta G_B^0}{RT}}]}{1-e^{-\frac{\Delta G_A^0+\Delta G_B^0}{RT}}}$

$LaTeX: x_A^\alpha=\frac{[1-e^{-\frac{\Delta G_B^0}{RT}}]}{1-e^{-\frac{\Delta G_A^0+\Delta G_B^0}{RT}}}$

Dies sind die beiden Gleichungen zur Berechnung der Liquidus- und Solidus-Linie. In der Aufgabe 12.5 werden einige Beispiele gezeigt.

Eine ausführlichere Begründung findet man in dem Übersichtsartikel von D.Gaskell in R.Cahn and P.Haasen 'Physical Metallurgy' North Holland Publishing, Amsterdam 1983.

Aufgabe 12.2:

Kalorimetrische Bestimmung der Phasengrenzen

Es gibt viele Methoden zur Messung der Phasengrenzen wie NMR-und Infrarot-Spektrokopie, Kalorimetrie und Densitometrie. Wir betrachten nur die beiden letzteren Verfahren:

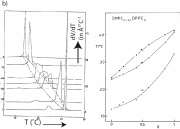
Differentialkalorimetrie: Die Methode wurde in Aufgabe 10.3 ausführlich beschrieben. Die Meßgröße ist $LaTeX: \Delta H = \int_{T1}^{T2}C_pdT=\int_{t1}^{t2}\frac{dH}{dt}dt$ . Da beim Aufwärmen an der Solidus-Kurve abrupt Wärme frei wird, steigt $LaTeX: C_p = \frac{dH}{dT}$ steil an. Beim Überschreiten der Liquiduskurve tritt wieder eine Überhöhung der $LaTeX: C_p$ -T auf, da die frei werdend Wärme wieder abrupt auf null abfällt. Die Breite des Anstiegs und des Abfalls ist durch die Breite der Umwandlung der reinen Komponente bestimmt. In der Mitte der Zigarre ändert sich Cp langsam und es entsteht eine Eindellung der $LaTeX: C_p$ -T-Kurve. Das mittlere Bild zeigt die gemessene und berechnete $LaTeX: C_p$ -T-Kurven für die Mischung aus DMPC und DPPC und das daraus berechnete Phasendiagramm. Die Theorie zur Bestimmung von $LaTeX: C_p$ wurde in der Arbeit von Mabrey and Sturtevant dargestellt.

Verallgemeinerte Darstellung

DMPC DPPC Kalorimetriekurven

DMPC DPPC Phasendiagramm

Die Densitometrie ist eine andere klassische, aber sehr empfindliche thermodynamische Methode zur Bestimmung der Phasendiagramme. Dabei wird die Dichte der Lösungen bestimmt, indem man die Verstimmung eines zu mechanischen Schwingungen angeregten Oszillators misst. Als solcher dient beispielsweise ein Glasröhrchen, das mit der Substanz befüllt wird, deren Masse M genau bekannt ist. Die effektive Masse des schwingenden Systems ist dann $LaTeX: m_{eff} = m_0+\rho V$ , wobei $LaTeX: \rho$ die Dichte und V das Volumen der Substanz sind. Im Fall ungedämpfter Schwingungen ist die Eigenfrequenz $LaTeX: \omega = \sqrt{ \frac{k}{m_0}}=\sqrt{ \frac{k}{M + \rho V}}$ , wobei k eine Federkonstante des Systems ist, die man durch Messung der Masse des leeren Röhrchens bestimmt.

Quellen: Calorimetrie DMPC/DPPC: S. Mabrey and J. Surtevant, Proc.Natl.Acad Sci 73,3863 (1976)

Densitometrie: G. Schmidt and W. Knoll, Berichte Bunsenges. Phys Chem 89; 36-43, 1985.

Aufgabe 12.3:

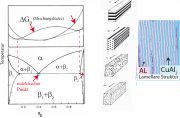
Eutektikum (griechisch: 'gut schmelzen') ist ein Phasengleichgewicht einer binären Mischung, in dem drei Phasen im Gleichwicht koexistieren. Die linke Abbildung zeigt die Entstehung eines Eutektikums im Bild der freien Energie als Funktion der Zusammensetzung.

Schematische Darstellung der Mischungslücke und Strukturen

Eutektische Mischungen findet man in der Regel nur bei Metalllegierungen. Sie sind aus zwei Gründen interessant:

- Der Schmelzpunkt eutektischer Legierungen liegt sehr tief. Beispiel ist Lötzinn, eine Legierung aus Sn und Pb mit 62\

- Eutektische Mischungen können sehr vielfältige Strukturen durch hochgeordnete Anordnungen der Mischphasen ausbilden. Das Bild zeigt zwei Beispiele: Links sehen wir typische geordnete Strukturen, die beim Abkühlen aus dem eutektischen Punkt entstehen können. Es handelt sich um ein interessantes Problem der Musterbildung durch Zusammenspiel von Diffusion und Grenzflächenkräften an den Phasengrenzschichten. Das rechte Bild zeigt das reale Beispiel einer Al/Cu-Legierung, wobei die feste Phase aus einer stöchiometrischen $LaTeX: CuAl_2$ -Mischung und die fluide aus flüssigem Al besteht (Schmelzpunkte: Al ca 600°C, Cu ca 1000°C). Die Metallurgen benutzen diese Möglichkeit, um Metalle mit spezifischen mechanischen Eigenschaften herzustellen, beispielsweise um die Formbarkeit (Duktilität, engl. ducility genannt) zu erhöhen. Ein wichtigs Beispiel ist die eutektische Mischung aus 72\

- Es gibt auch interessante Anwendungen eutektischer Mischungen zur Anwendung von Arzneimitteln (ein Galenik genanntes Gebiet, auf dem auch Physiker gefragt sind), wo es darum geht, die Pharmaka möglichst an spezifischen Stellen des Körpers zu konzentrieren, um die Dosis gering zu halten. Ein erfolgreiches Beispiel ist die Applikation von Lokalanästhetika auf der Haut. Die Wirkstoffe Lidocaine and Prilocaine werden in Emulsionen suspendiert. Werden die Substanzen getrennt eingebracht, bleiben sie kristallin. 1:1 Mischungen bilden dagegen bilden eine eutektische Mischung und sind bis 18 ° C fluide.

Zusatzbemerkung: Es mag etwas absurd erscheinen, in einem Buch über Biophysik Beispiel aus der Metallphysik zu diskutieren. Da man es in der Biologie stets mit Verbundmaterialien aus vielen Komponenten zu tun hat, spielt die Physik von Mischsystemen eine zentrale Rolle für deren Struktur und Funktion, wie das Beispiel der Bildung von funktionalen Domänen zeigt. Viele Millionen Jahre der Evolution waren notwendig, um die richtigen Membranmischungen und Methoden zur Kontrolle der Zusammensetzung auszubilden. Die Metallurgen haben dank der Thermodynamik der Mischungen seit rund 150 Jahren gelernt, Mikrostrukturen der Metalle systematisch einzustellen, um spezifische physikalische Eigenschaften zu erzwingen. Man denke nur an die Herstellung von rostfreiem Stahl. Natürlich haben die Menschen auch vorher schon intuitiv erstaunliche Legierungen (wie Bronze und Stahl) hergestellt, aber die Entwicklung ging sehr viel langsamer.

Die Metallphysik ist ungeheuer reich an Beispielen, an denen man die Grundprinzipien der Physik von Legierungen lernen und verstehen kann, um neue Materialien rational zu entwickeln. Wenn wir Zusammenhänge zwischen der Struktur und Funktion der Membranen, des Zytoskeletts oder der extrazellulären Matrix quantitativ erfassen wollen, müssen wir die Thermodynamik der Legierungen aus Lipiden und Proteinen oder der Mischungen aus semiflexiblen und flexiblen Polymeren systematisch untersuchen. Die rationale Herstellung biologischer oder biokompatibler Materialien ist ein zukunftsträchtiger Zweig der angewandten Biomaterialforschung.

Aufgabe 12.4:

Aufbau von Modellmembranen-Rekonstitution von Proteinen.

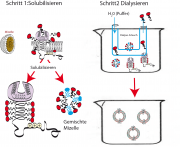
Motivation: Eine Strategie auf dem Weg zum Verständnis komplexer Biomaterialien ist der Aufbau zunehmend realistischer Modelle. Um Zusammenhänge zwischen Struktur und Funktion einzelner Membranpoteine zu verstehen, werden diese in Vesikel oder festkörpergestützte Membranen eingebaut (siehe Abb 13.3), ein oft sehr mühsames Verfahren. Es besteht aus zwei Schritten: Der Solubilisierung der Proteine und Phospholipide durch Tensiden (engl. surfactants) und der anschließenden Entfernung der Tenside. Wie in der Abbildung links oben dargestellt, wird der hydrophobe Stamm der Proteine durch einen Mantel aus Tensiden umgeben und so dessen Denaturierung vermieden. Wichtig ist die Verwendung von nicht-ionischen Tensiden, um die Denaturieung der Kopfgruppen der Proteine zu umgehen.

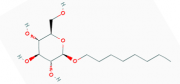
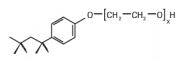
Zwei wichtige Beispiel sind:N-Octyl- $LaTeX: \beta$ -D-glucoside (mit der kritischen Mizellkonzentration (cmc) von 6 to 8 mM ) und Triton X100 (cmc 23 mM):

N-Octyl- $LaTeX: \beta$ -D-glucoside

Triton X100

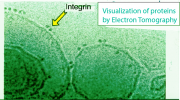
Durch sukzessive Entfernung der Tenside entstehen die Vesikel mit eingebauten Proteinen durch Selbstorganisation. Den Beweis des Erfolgs des Experiments führt man in der Regel mittels Elektronenmikropskopie, insbesondere Elektronen-Tomographie. Das rechte Bild zeigt in Vesikel eingebaute Integrin-Rezeptoren (nicht veröffentlichen Aufnahmen eines Autors (ES)). Aus solchen Aufnahmen folgt, dass mit den Methoden ein Protein-zu-Lipid-Verhälnis von etwa $LaTeX: 10^{-3}$ erreicht wird. Dies entspricht in etwa den Dichten einzelner Sorten von Membranproteinen in Zellmembranen (z.B. von Bande III- Proteinen in Erythrozyten s. Kapitel 12 oder von Selektinen in Leukozyten).

Dialyseverfahren

Elektronentomographisches Bild eines (Integrin) Proteins

Grundlagen der Dialyse-Methoden und Alternativen: Der Grund für die Bildung der Membranen ist die extrem niedrige cmc der Phospholipide von cmc ~ $LaTeX: 10^{-12 } M^{-1}$ , verglichen mit dem Wert der Tenside: cmc~ $LaTeX: 10^{-3}M^{-1}$ . Neben den Mischmizellen aus Tensid, Phospholipid und Protein enthält der Puffer in der Präparationszelle einige mM des molekular gelösten Tensids. Ersetzt man dieses Lösungsmittel durch reines Wasser, so werden die monomeren und in Mizellen befindliche Tenside durch die Poren der Dialysemembran entfernt und Vesikel mit eingebauten Proteinen werden gebildet.

Manche Tenside wie Triton X100 lassen sich schwer durch Dialyse entfernen. Daher benutzt kolloidale Suspensionen von Polymer-Partikeln (z. B, die kommerziell erhältlichen Biobeads), welche Triton sehr stark adsorbieren. Man trennt dann die Vesikeln von den Kolliden durch Zentrifugation.

Aufgabe 12.5:

Spontane Porenbildung in Membranen.

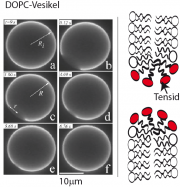
Die Bildung von Poren in Lipid-Vesikel ist von praktischer Bedeutung. Sie spielt eine wichtige Rolle bei der Herstellung festkörpergestützter Membranen durch Spreiten von Vesikeln auf Festkörpern und bei der Freisetzung von Wirkstoffen aus Vesikeln, bei deren Anwendung als Arzneimittel-Transporteure in Zellen. Schließlich haben wir die Bedeutung der Porenbildung als letzten Schritt vor der Fusion von Membranen kennengelernt. Es gibt zwei Wege zur Steuerung der Porenbildung: Die Erhöhung der lateralen Spannung $LaTeX: \sigma$ und die Reduktion der Randenergie der Poren durch Tenside. Wir betrachten hier nur den ersten Fall. Ein sehr schönes Experiment zur Porenbildung stammt von der Arbeitsgruppe von F. Brochard. (E. Karatekin, Biophys. J 84, 1734 (2003)). Ein Beispiel aus dieser Arbeit zeigt die Abb. 12.5A. In dieser wurde die Membranspannung durch Erhöhung des osmotischen Drucks mittels Glukose kontrolliert. Zur Verlangsamung des Prozesses wurde Glyzerin zum Puffer gegeben (Viskosität $LaTeX: \eta=32 \cdot 10^{-3} \frac{Js}{m^2}$ oder 32cP). Die Vesikel wurden mit fluoreszierenden Lipiden dotiert und mittels Mikrofluoreszenz beobachtet.

Spontane kurzzeitige Porenbildung in DPOC-Vesikeln. Man beachte, dass die Pore sich kurzfristig öffnet und wieder schließt.

Definition der projizierten rauen Fläche. Dabei ist u ist die Ondukatioinsamplitude.

Mechanik der Porenbildung durch laterale Spannungen. In Kapitel hatten wir darauf hingewiesen, dass die dynamisch rauen Membranen durch laterale Spannungen geglättet werden. Zur quantitativen Analyse dieser Glättung hatten wir die Differenz $LaTeX: \delta A$ zwischen den Flächen einer glatten (Fläche $LaTeX: A_0$ ) und einer rauen Membran ( $LaTeX: A_p$ ) betrachtet. Wir hatten begründet, dass die relative Flächenänderung $LaTeX: \frac{\delta A}{A}$ bei Anlegen einer kleinen Membranspannung $LaTeX: \sigma$ ' durch Gleichung 11.5b gegeben ist.

$LaTeX: \frac{\delta A(\sigma)}{A_0}\approx -\frac{k_BT}{8\pi \kappa}ln(\frac{\kappa \pi^2}{\sigma ' d_m^2})$ (1a)

Dabei $LaTeX: \frac{\pi}{d_m}$ der Wellenvektor der höchsten Mode und $LaTeX: d_m$ die Membrandicke. Diese Gleichung wurde in einer Arbeit von Servus und Helfrich (in Il Nuovo Cimento 3D, 137, 1984) abgeleitet. In derselben Arbeit wurde für den Fall der spannungsfreien Membran folgende Gleichung abgeleitet:

$LaTeX: \frac{\delta A(\sigma)}{A_0}\approx -\frac{k_BT}{8\pi \kappa}ln(\frac{ A_0 \pi^2}{d_m^2})$ (1b)

Wir betrachten im folgenden den einfachen Fall einer flachen Membran. Der komplizierte Fall eines sphärischen Vesikels wurde in der Arbeit von Karatekin et al (Biophysical J 84,1734-1749 (2003)) behandelt. Der Beitrag der Biegeenergie zur Porenbildung ist jedoch klein.

Wenn wir nun die Membran durch Variation des osmotischen Druckes oder mittels Mikropipetten dehnen, so hat die relative Dehnung die Form $LaTeX: \eta= \frac{\delta A(\sigma)}{A_0 } - \frac{\delta A(0)}{A_0}$ . Setzt man die Gln.(1a) und (1b) ein und berücksichtigt, dass bei $LaTeX: \sigma=0$ auch $LaTeX: \eta =0$ wird, so folgt:

$LaTeX: \eta\approx\frac{k_BT}{8\pi \kappa}ln(1+ \frac{\pi^2 \sigma ' A_0}{\kappa})$

a) Die Biegeenergie quasisphärischer geschlossenen Membranen ist unabhängig vom Radius R und beträgt: $LaTeX: \Delta G_{ela} = 8\pi \kappa$ . Für Phospholipid-Vesikel ist $LaTeX: \kappa$ ~ $LaTeX: 10 k_BT$ , d.h. die gesamte Energie beträgt nur einige $LaTeX: k_BT$ und ist klein gegenüber der Randenergie, die beim Öffnen der Pore aufgewendet werden muss.

b)Wird die geglättete Membran weiter gestreckt, so muß man dies durch einen zusätzlichen Beitrag berücksichtigen. Die allgemeine Dehnungs-Kraft Beziehung lautet daher:

$LaTeX: \eta\approx\frac{k_BT}{8\pi\kappa}ln(1+\frac{\pi^2\sigma ' A_0}{\kappa})+\frac{\sigma}{K}$

wobei K der Kompressionsmodul der Membran ist.

Darstellung der Energie der Pore als Funktion des Porenradius.

Eine ausführliche Theorie der Kinetik des Öffnens und Schließens von Poren findet man in der Arbeit von Karatekin et al (2003).

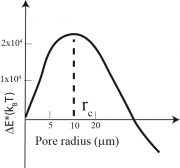
c) In Kapitel 12.6 hatten wir die Bildung von Poren als aktivierten Prozess beschrieben und gezeigt, dass der Aufwand an Randenergie durch die Reduktion der Spannung (und damit der in der Membrandehnung gespeicherten Energie) aufgrund der Verkleinerung der Vesikelfläche kompensiert wird. Diese Betrachtung lieferte folgende Gleichung für den kritischen Radius: $LaTeX: \rho * =\frac{\Gamma}{4\sigma}$

Mit $LaTeX: \sigma = 10^{-6} \frac{N}{m}$ wird $LaTeX: \rho *$ ~ $LaTeX: 2 \mu m$ . Der experimentelle Wert nach Karatekin ist größer(~ $LaTeX: 10 \mu m$ ). Mit dem unten abgeschätzen Wert von $LaTeX: \Gamma$ wird $LaTeX: \rho$ *~ $LaTeX: 10\mu m$ .

Warum schließt die Pore wieder?

Wenn die Pore öffnet, wird aufgrund des Laplace- Drucks ( $LaTeX: P=2\frac{\sigma}{R}$ ) Wasser aktiv ausgetrieben. Die Membran-Spannung relaxiert und die Pore schließt sich wieder.

Abschätzung der Randenergie G: Man kann die Randenergie aus der Bindungsenergie $LaTeX: \delta e$ der Lipide in Membra abschätzen. Diese wurde mit der Kraftspektroskopie mittels Mikropipetten bestimmt (Abb. 8.10 und Evans und Ludwig, J. Phys. Condensed Matter. 11, 1-6 (1999)) und liegt bei mittleren Kraftraten bei rund 25 pN. Mit $LaTeX: d_m \approx 4nm$ wird $LaTeX: \delta e \approx 25 k_BT$ . Der Porenradius sei ~ 50 nm (Umfang ~ 300 nm) und enthält ~ 300 Lipide: d.h. $LaTeX: \Gamma$ ~ 25 pN. Dieser Wert stellt eine obere Grenze von $LaTeX: \Gamma$ dar, da nur eine Kette mit Wasser in Kontakt kommt, wenn sich die Pore öffnet.

Search

Navigation

SEARCH

TOOLBOX

LANGUAGES