Lösungen Kapitel 14

From BioPhy.de Wiki

Aufgabe 14.1:

Das Planck'sche Diffusionspotential-wo ist es wichtig?

Bei der Berechnung der stationären Membranpotentiale geht man immer davon aus, dass die beteiligten Ionen in der Zelle und der extrazellulären Matrix homogen verteilt sind. Lokale Konzentrationsgradienten und die unterschiedliche Beweglichkeit der Ionen werden vernachlässigt.

In Gegenwart mehrerer Sorten von Ionen mit unterschiedlichen Beweglichkeiten kann an Grenzflächen zusätzlich das Planck'sche Diffusionspotential auftreten. Dazu betrachten wir als Beispiel ein Salz (Konzentration $LaTeX: c_S$ ), das in $LaTeX: \nu_A$ Anionen der Wertigkeit $LaTeX: z_A$ und $LaTeX: \nu_K$ Kationen mit $LaTeX: z_K$ dissoziiert sei.

$LaTeX: A_{\nu_A}K_{\nu_K} \longleftrightarrow \nu_A A^{-z_A}+ \nu_K K^{+z_k}$

Daher gilt $LaTeX: c_A= \nu_Ac_S$ und $LaTeX: c_K= \nu_K c_S$ . Wie in Kapitel 14 gezeigt, müssen wir die Bedingung der Elektroneutralität an jedem Ort erfüllen:

$LaTeX: c_K z_K =c_Az_A$

$LaTeX: j_j=c_ju_j \nabla\mu^{elechem} = -u_jc_j (\frac{\partial \mu}{\partial x} + z_j e \frac{\partial \Phi}{\partial x}) = u_j c_j (k_B T \frac{\partial ln(c_i)}{\partial x}+z_i F \frac{\partial \Phi}{\partial x})$

Eine analytische Lösung des Problems ist nur für den stationären Zustand der Ströme der positiven und negativen Ionen möglich. Dazu müssen sich die Ströme gemäß $LaTeX: j_K z_K=j_Az_A$ kompensieren:

$LaTeX: \frac{\partial \Phi}{\partial x}= -\frac{u_K - u_A}{u_Kz_K + u_Az_A} \frac{k_BT}{e}\frac{\partial ln(c_S)}{\partial x}$

Anwendungen: Betrachten wir den Fall der Erythrozyten in physiologischer Kochsalzlösung. Diese enthält 145 mM NaCl. Die Beweglichkeiten $LaTeX: u_i$ durch die Membran ist durch die Permeabilität $LaTeX: P_i=\frac{D}{d_m} = \frac{u}{k_BT d_m}$ gegeben. Nach 14.3.7 verhalten sich die Permeabilitäten durch die Membrane wie $LaTeX: P_{Na}: P_{Cl}= 0.04:0.45$ .

Im Inneren der Zelle ist die Salzkonzentration nach Abbildung 9.8 etwa 50 mM. Daher wird $LaTeX: \partial ln(c_S) \approx ln(3)$ mit $LaTeX: k_BT \approx 25 meV$ und $LaTeX: \Delta \Phi_{Planck} \approx -20 mV$ .

Aufgabe 14.2:

Wie der junge Helmholtz die Geschwindigkeit der Nervenimpulse bestimmte.

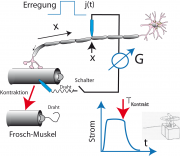
Bis 1852 nahm die Mehrheit der Naturforscher noch an, die Erregung der Nervenleiter würden sich extrem schnell (evtl. mit Lichtgeschwindigkeit) ausbreiten. Die Meinung geht insbesondere auf Newton zurück. Der junge Helmholtz muss ein mutiger Mann gewesen sein, als er daran ging, diese Hypothese zu widerlegen. Besonders beeindruckend und lehrreich ist die Idee, die er zur Durchführung des Experiments entwickelte. Eine mögliche schematische Ansicht der Anordnung zur Messung von Helmholtz zeigt die Abbildung unten links. Durch die Kontraktion des Muskels reißt die elektrische Verbindung (ein dünner Draht) zwischen dem Muskel und dem motorischen Axon und unterbricht den Stromkreis. Man kann den Anstieg und Abfall des Stromes mit einem ballistischen Galvanometer beobachten.

Experiment zur Muskelkontraktion von Helmholtz

Helmholtz benutzte für das erste Experiment tatsächlich einen Wellenschreiber (Kymograph), ein auf Thomas Young zurückgehendes Gerät zur schnellen Registrierung der Position eines Zeigers mit der Zeit. Es besteht aus einer rotierenden Walze, die mit Ruß bedeckt ist und auf der ein Zeiger (Griffel) die Position als Funktion der Zeit einritzt. Eine Skizze des Aufbaus zeigt die obige Abbildung rechts.

Aufgabe 14.3:

Wie Synapsen durch Abbau der Transmitter die Übertragungsrate beschleunigen.

Die Breite der Synapse sei etwa 1000 nm:

Elektronenmikroskop Bild einer Synapse und schematische Zeichnung

Lösung: Mit der effektiven Viskosität der Flüssigkeit im Spalt von $LaTeX: \eta_{eff} \approx 10^{-2}$ Pas wird $LaTeX: D_{eff} \approx 10^{-6} \frac{cm^2}{s}$ .Unter der Annahme, dass das Gewebe im synaptische Spalt homogen ist, kann die Zeit, die ein Molekül braucht, um die Strecke r vom Zentrum zum Rand zu diffundieren, einfach aus der Einsteinbeziehung abschätzen. Wir nehmen dabei an, dass der Spalt so breit ist, dass man die Diffusion als dreidimensional beschreiben kann. Dann wird $LaTeX: t = \frac{<r^2>}{4D} \approx 2.5 ms$ . Das ist relativ schnell, aber bei hoher Aktivität reichert sich der Transmitter mit der Zeit an. Die Viskosität $LaTeX: \eta_{eff}$ ist wahrscheinlich auch etwa 10 mal größer.

Es gibt mehrere Publikationen mit exakteren Berechnungen des Diffusion in synaptischen Spalten. Das Problem der Diffusion des Acetylcholins wurde von Anthony und Aidoo, behandelt (Mathematical and Computer Modelling 44: 952-962, (2006)). J. Kleinle et al. (Biophysical J 71, 2413 (1996)) berechnete die zeitliche Verteilung der durch Vesikelfusion an der Oberfläche der prä-synaptischen Membranlokal erzeugten Transmitters. Sie behandeln vor allem das Problem der Sättigung der Rezeptoren mit Transmitter.

Ergänzung zum Auf- und Abbau des Acetylcholins:

Der Transmitter kommt im ganzen Tierreich (im autonomen vegetativen und im motorischen Nervensystem) vor. Die Synthese findet in den Nervenzellen statt und wird in 30-60 nm großen sekretorischen Vesikeln gespeichert. Es gehört zu den aktiv, d.h. durch die Erhöhung des Ca-Spiegels, ausgeschütteten Hormonen, so wie Adrenalin.

Der Abbau findet durch die Acetylesterase im zytoplasmatischen Spalt statt. Das Enzym ist eines der schnellsten, die man bisher kennt. Es spaltet den Transmitter in Essigsäure und Cholin. Die externe Hemmung des Enzyms, durch Pestizide oder Giftgase (wie Sarin) hat fatale Folgen. Die dadurch bedingte Anreicherung des Transmitters im synaptischen Spalt führt zu Krämpfen oder Tod durch Atemlähmung.

Aufgabe 14.4:

Experimenteller Beweis der Ca-induzierten Fusion synapticher Vesikel.

Wir beschreiben hier die Methode nach K. R. Delay und R. S. Zucker (Journal of Physiology 426; 473-498, (1990)). Zum Beweis der Hypothese benutzten Zucker et al. die Methode der Freisetzung der Ca-Ionen aus gefangenen Verbindungen. Bei dieser weiter unten beschriebenen Technik injiziert man Komplexierungen mit Ca (sog. Chelate) in die Synapsen. Durch Belichtung mit einem Lichtblitz (der Wellenlänge $LaTeX: \lambda \leq 350 nm$ ) wird Ca freigesetzt.

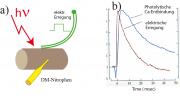
Abbildung 14. A1 zeigt das Ergebnis dieses eleganten Experiments. In diesem beobachtet man die Erregung der postsynaptischen Membran einmal nach Anregung eines elektrischen Impuls $LaTeX: \Delta V$ und nach Belichtung mit einem Lichtimpuls von $LaTeX: \lambda = 350 nm$ . Die Aktionspotentiale der postsynaptischen Membran sehen sehr ähnlich aus, abgesehen von der etwas langsameren und unvollständigen Relaxation im Fall der photolytischen Ca-Freisetzung. Der Grund liegt darin, dass der dissoziierte Ca-Komplex als Puffer wirkt, der den intrazellulären Kalziumspiegel über dem Wert der Zelle im Ruhezustand (d.h. $LaTeX: ~10^{-7}$ M) festklemmt.

Photolyse DM-Nitrophen

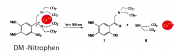
Photolytische Freisetzung von Ca Ionen aus einem organischen Ionenkomplex (engl. caged Ca-compound). Die photolytische Entbindung von gefangenen Verbindungen (wie ATP) oder Ionen (wie $LaTeX: Ca^{2+}$ ) ist eine elegante Methode zur lokalen Freisetzung von Energie (wie ATP) oder Botenmolekülen (wie $LaTeX: Ca^{2+}$ oder c-AMP). Zur lokalen Applikation von Ca benutzt man häufig die unten gezeigte Verbindung: 1-(2-nitro-4,5-dimethoxyphenyl)-N,N,N',N'-tetrakis[(oxycarbonyl)methyl]-1,2-ethanediamine (Abkürzung DM-Nitrophen). EPSP (excitatory postsynaptic potential): Abkürzung für das exzitatorische Potential an der postsynaptischen Membran.

Abbildung 14. A 3: Chemische Struktur des Ca-Cheators DM-Nitrophen und der Spaltung des Komplexes durch Anregung mit Licht der Wellenlänge $LaTeX: \lambda \approx 350 nm$ . Nach Kaplan und Ellis-Davies (PNAS 85, (1988))

Die Bindungskonstante des Chelators beträgt $LaTeX: K_a \approx 5 nM$ . Daher ist im Ruhezustand der Zellen (bei der Ca-Konzentration $LaTeX: 0.1 \mu M$ ) Kalzium im Komplex gebunden. Nach der Spaltung des Komplexes bindet Ca sehr schwach (mit $LaTeX: K_a* \approx 2.5 \mu M$ ). Daher wird der intrazelluläre Ca Spiegel erhöht, auf zwar bis auf den Wert $LaTeX: K_a*$ bzw. der Konzentration des Chelators, falls diese höher ist, als die Ca- Konzentration im Ruhezustand der Zelle.

Ergänzung zur Aufgabe 14.4: Ein eleganter Nachweis, dass Ca die Vesikelfusion einleitet und dass dies nahe am Ort der Fusion stattfinden muss, zeigt ein einfaches elegantes Experiment von Adler et al. (Adler et al. J Neuroscience 11: 1496-1507 (1991)). Es basiert auf der Verwendung der beiden Chelatoren BAPTA und EGTA, BAPTA bindet Ca sehr stark (mit $LaTeX: K_d= 2 10^{-7}$ ) und vor allem sehr schnell; mit einer Bindungsrate von $LaTeX: k_+=5 \cdot 10^8 \frac{1}{M s}$ . EGTA bindet ähnlich stark, aber 100 mal langsamer ( $LaTeX: k_+=10^6 \frac{1}{M s}$ ). Im Experiment wurden die Chelatoren in die Synapsen injiziert und das exzitatorische postsynaptische Potential (EPSP) gemessen, mit folgendem Ergebnis (Bilder siehe Nicholls et al. 'From Neuron to Brain' Ch. 11 'Transmitter release'):

Der schnelle Chelator BAPTA unterdrückt das postsynaptische Potential (EPSP), das langsamere EGTA dagegen nicht. Durch sorgfältige Analyse der Kinetik der Ca-Bindung und der Diffusion der Chelatoren in den Synapsen konnten Adler et al. zeigen, dass der Ca-Kanal, durch den die Ionen eintreten und der Ort der Fusion nicht mehr als 100 nm voneinander entfernt sein können. Dies Experiment ist erwähnenswert, denn es zeigt eindrucksvoll, wie man durch geschickte biophysikalische Experimente quantitative Information über molekulare Prozesse auf nm-Skalen in Zellen gewinnen kann. Die Analyse basiert etwa auf folgender Betrachtung: Wenn Ca durch die Kanäle eintritt, benötigt es die Zeit $LaTeX: t \approx 10^{-5} s$ , um 100 nm zu diffundieren (Diffusionskoeffizient $LaTeX: D=10^{-6} \frac{cm^2}{s}$ ). Ist die Synapse mit BAPTA gefüllt, so wird Ca (Konzentration c) mit der Rate $LaTeX: \frac{dc}{dt}=k_+c_Bc$ gebunden. Daher $LaTeX: c(t)=c_oexp^{-tk_+c_B}$ . Ist $LaTeX: c(0) = 10^{-5} M$ ( $LaTeX: 100 \mu M$ ), so erfolgt die Bindung in $LaTeX: t \approx (k_+c(0))^{-1} \approx 10^{-5} s$ , d.h. BAPTA kann fast alle Ca-Ionen binden, ehe diese 100 nm diffundiert sind. Das 100 mal langsamer bindende EGTA kann dies nicht.

Aufgabe 14.5:

Das Quantengesetz der postsynaptischen Erregung.

Vorbemerkungen: Die Beobachtung der Erregung der postsynaptischen Membran durch simultane Freisetzung einer minimalen Menge von Transmittern (die Transmitter-Pakete oder Quanten) geht auf B. Katz (del Castillo and B. Katz. (1954)). Sie gehört zu den wichtigsten Entdeckungen der Neurophysik. Der Bezug zur Quantenmechanik ist eher symbolisch zu verstehen. Allerdings besteht eine Analogie darin, dass ein gewisses Quantum an Transmittern notwendig ist, um ein anderes Neuron oder eine Muskelfaser in einen aktiven Zustand zu versetzen. Die Entdeckung von B. Katz und J. del Castillo ist ein lehrreiches Beispiel dafür, wie man aus einfachen Experimente und durch Nachdenken quantitative Biologie betreiben kann.

Die Entdeckung des Quantengesetzes basierte auf einer sorgfältigen Analyse der durch Nervenimpulse induzierten Potentiale der Muskel-Endplatte. Letztere wurde durch Mikroelektroden bestimmt (s. Abb. 14.A.5.1a). Tatsächlich sind Membranen für den Transmitter Acethylcholin (ACh) durchlässig und dessen passiver Strom ist 100 mal größer als der die durch ACh- Quanten vermittelte Ausschüttung. Wir haben aber in Abb.14.3 gesehen, dass der Transmitter durch das Enzym Acethylcholinesterase (durch Hydrolyse) wieder abgebaut wird, wodurch der ACh-Spiegel im synaptischen Spalt niedrig gehalten wird.

Abb. 14.A.5.: Zum Nachweis der Erregung der postsynaptischen Membran durch Freisetzung von Acetylcholin-Quanten; Am Beispiel der Muskel-Endplatte. (a) Messung der Spannung der Muskelendplatte mittels Mikroelektrode. (b) Spontane Aktionspotentiale der Muskelendplatte (auch Miniaturpotentiale genannt). Man beachte, dass deren Amplituden etwa 1 mV betragen. (c)Überlagerung von drei beobachteten Endplattenpotentialen (EPP) deren Amplituden sich ungefähr wie 1: 2: 3 verhalten. (d) Verteilung der Amplituden der Endplattenpotentiale an einer Muskelendplatte bei hoher Konzentration von Magnesium gemessen ( $LaTeX: \approx 12 mM$ ). Man beachte, dass das Histogramm deutliche Maxima bei 0.4, 0.8 und 1.2 mV zeigt. Die Balken geben die Messungen wieder und zeigen die experimentell gemessenen Häufigkeiten. Die ausgezogene Kurve zeigt den nach der Poissonverteilung erwarteten Abfall der Wahrscheinlichkeit, dass ein, zwei oder drei ACh- Pakete gleichzeitig ausgeschüttet werden.

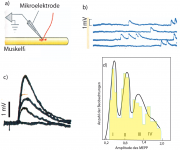
Experimente und Analysen.

Da man wusste, dass die post-synaptische Erregung durch Ca-Ionen ausgelöst wird, wurde Kalzium im Außenmedium durch Mg- Ionen ersetzt, um die physiologischen elektrischen Bedingungen zu erhalten. Gleichzeitig wurde die Stärke der elektrischen Stimulation der Muskelendplatte so weit reduziert, dass einzelne Erregungen der Membran beobachtet werden konnten (siehe Abb. 14.A.5b). Del Castillo und Katz verglichen die durch Nervenimpulse und durch spontane Erregung ausgelösten Aktionspotentiale der Muskelfasern. Die überraschende Beobachtung war, dass die beobachteten Aktionspotentiale (die Endplatten-Potentiale EPP) Vielfache eines minimalen Potentials (dem Miniatur Endplatten-Potential MEPP) sind. Die Amplituden der MEPP sind 1 mV (s. Abb. 14. A.5c).

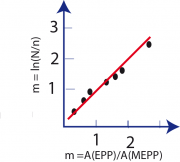
Die Messung vieler Potentiale ergab das in der folgenden Abbildung gezeigte logarithmisches Gesetz für das Verhältnis der Amplituden der gemessenen Potentiale A(EPP) zum Miniaturpotential A(MEPP):

$LaTeX: m= \frac{A(EPP)}{A(MEPP)}=ln(\frac{N}{n})$ oder $LaTeX: n=Ne^{-m}$

Wobei N und n rationale Zahlen sind.

Amplitudenverhältnis EPP/MEPP

Del Castillo und Katz schlossen aus diesem Ergebnis, dass die präsynaptische Membran tausende von Paketen aus ACh enthält, die mit einer gewissen Wahrscheinlichkeit p in den synaptischen Spalt freigesetzt werden und die Muskelmembran erregen, wobei sie annahmen, dass jedes Paket dieselbe Menge an Transmittern erhält. Da die Existenz der synaptischen Vesikel noch unbekannt war, war dies eine gewaltige Leistung.

Das Modell beruhte auf der genialen Idee, dass die statistische Ausschüttung der Transmitter durch die Poisson-Stastistik bestimmt ist. Die Poisson-Verteilung ist eine Näherung der Binominalverteilung für kleine Wahrscheinlichkeiten p. Sie hat gegenüber dieser den großen Vorteil, dass man weder die Gesamtzahl der Pakete N (d.h. die Zahl synaptischer Vesikel) noch die Wahrscheinlichkeit p der Öffnung a priori wissen muss, sondern nur das Produkt Np, das gleich der mittleren Zahl der pro Versuch geöffneten synaptischen Vesikel oder gleich dem EPP ist.

Die Poisson-Verteilung hat hier folgende Form:

$LaTeX: n=N(\frac{\lambda^k}{k!})e^{-\lambda}$ oder $LaTeX: \lambda=ln(\frac{m^k}{k!})+\frac{N}{n}$

Trägt man also das Amplitudenverhältnis $LaTeX: m=\frac{A(EPP)}{A(MEPP)}$ gegen das Zahlenverhältnis $LaTeX: \frac{N}{n}$ auf, so liegen die Messpunkte auf eine Geraden. Wie Abb 14 A.5d zeigt, folgt die Wahrscheinlichkeit, dass ein, zwei oder drei synaptische Vesikel gleichzeitig mit der präsynaptischen Membran fusioniert sind, in der Tat einer Poisson-Verteilung.

Messung der Zahl der ACh- Moleküle pro Paket. In der ersten Messung wurden sehr feine Pipetten mit definierten Mengen an ACh gefüllt und auf Muskelendplatten gespritzt (siehe Nicholls et al, Seite 211). Der Vergleich der mit dieser Methode erzeugten Antworten der Muskelendplatte mit den unter physiologischen Bedingungen erzeugten Erregungen zeigte, dass pro Paket etwa 7000 ACh-Transmitter ausgeschüttet werden. Die Zahl der Moleküle pro Paket ist im Fall des Muskels besonders groß.

Die Erregung von Ganglion-Zellen erfolgt dagegen mit rund 10 Transmittern und in den Zellen des Zentralnervensystems sind nur wenige Transmitter (manchmal nur einer) beteiligt. Da in diesen Fällen die Wahrscheinlichkeit der Öffnung der Kanäle jedoch groß ist $LaTeX: p\approx 0.9$ ist, reicht die geringe Menge an Transmittern jedoch aus, um die Zielzelle zu depolarisieren. Hinzu kommt, dass jede Zelle Signale von vielen Synapsen erhält. Da p nahezu eins ist, lässt sich die Poissonverteilung nicht mehr anwenden, sondern man muss dann die Messungen mittels Binominalverteilungen analysieren. Oft muss man noch komplexere statistische Methoden anwenden (s. J.Bekkers Curr. Opin. Neurobiol. 4, 360, (1994)).

Wie viele Kanäle werden pro Paket geöffnet. Um diesen Parameter zu bestimmen, vergleicht man den pro MEPP fließenden Strom mit dem durch einen einzelnen Kanal fließenden Strom. Ersterer ist etwa 40 nS und letzterer etwa 30 pS. Ein Miniaturpotential in der Muskelmembran wird also durch Öffnung von etwa 1300 Kanälen erzeugt. Die Zahl geöffneter Kanäle hängt von der Größe der Zellen ab. Sie beträgt im Fall der Neuronen des Hippocampus nur etwa 20-50 Kanäle. Die Größe der Transmitterquanten ist mit der Zahl der Rezeptoren in der postsynaptischen Membran korreliert. In der Muskelendplatte sind zehntausende von ACh-Rezeptoren dicht gepackt (10000 pro $LaTeX: \mu m^2$ ) und die Zahl aktivierter ACh-Rezeptoren und damit die Signalstärke hängt von der Zahl der ACh pro Quantum ab. Im Hippocampus ist die Zahl der Rezeptoren klein (etwa 100 auf einer Fläche von $LaTeX: 0.4 \mu m^2$ ) und jeder Rezeptor wird aktiviert.

Search

Navigation

SEARCH

TOOLBOX

LANGUAGES