Lösungen Kapitel 21

From BioPhy.de Wiki

Aufgabe 21.1:

Ausgangspunkt der Aufgabe ist Gl 21.1,

$LaTeX: \Delta \mu_p = e \Delta \Psi k_BT ln{\frac{[H_o^+]}{[ H_i^+]}}$ (20.1)

wobei $LaTeX: \frac{[H_o^+]}{[ H_i^+]}$ das Verhältnis der pH-Werte im Innen- und Außenraum ist. Das Membranpotential im Normalzustand der Bakterien und 25 ° C sei $LaTeX: \Delta \Psi \approx -120 mV$ . Der pH-Wert des Zytoplasmas ist $LaTeX: pH = -log_{10} {[H_i]} = 7.7$ . Mit $LaTeX: k_BT(25$ ° $LaTeX: ) =25 m eV$ wird $LaTeX: log{\frac{[H_o^+]}{[ H_i^+]}} = pH_o - pH_i \approx log (e^{4.8})= 4.8 log (e) \approx 2.1$ oder $LaTeX: pH_o \approx 9.7$ . Man beachte, dass man die Protonenkonzentration im Außenraum erniedrigen muss, um die treibende Kraft durch das Membranpotential zu kompensieren.

Aufgabe 21.2:

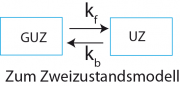
Einleitung: In Kapitel 21 haben wir gelernt, dass man den Wechsel von der Flagellen-Rotation im Uhrzeigersinn (ZU) zum Gegenzeigersinn (GUZ) als Übergang zwischen zwei thermodynamischen Zuständen verschiedener freien Energien beschreiben kann. Das ist erstaunlich, da wir es ja mit lebenden Systemen außerhalb des thermodynamischen Gleichgewichts zu tun haben. Der erste Schritt der Aufgabe besteht daher darin, die Experimente und deren Interpretation zu beschreiben, die Howard Berg und seine Arbeitsgruppe auf das Zweizustands-Modell brachten (siehe[1]). Die Experimente wurden mit der in Abb. 21.3a gezeigten Anordnung durchgeführt. Die Bewegung wurde in Gradienten aus attraktiven Aminosäuren (z.B. L-Serin) beobachtet wobei sich zeigte:

1. In homogenen Gradienten hoher mittlerer Konzentration C(x) bewegen sich die Zellen mit konstanter Migrations-Geschwindigkeit <v> zu hohen Konzentrationen. In Gradienten repulsiver chemotaktische Substanzen verharren die Zellen für lange Zeiten im Zustand der Taumelbewegungen, d. h die Flagellen bewegen sich im UZ. Auf molekularer Ebene bedeutet dies, dass die chemotaktischen Moleküle sehr lange an die Rezeptoren binden.

2. Liegt die mittlere Konzentration in der Nähe des Rezeptor-Liganden-Gleichgewichts, so ändern sich die Zustände zeitlich (mit einer gewissen Verzögerung im Zeitbereich von Sekunden) proportional mit $LaTeX: \frac{d(log C)}{dt}$ . Daraus kann man schließen, dass die Zellen das Eingangssignal (=ES; d. h. die Zahl besetzter Rezeptoren) über eine gewisse Zeit integrieren.

3.Andere Beobachtungen zeigen, dass die Zellen die zeitlich Ableitung des ES verarbeiten. Diese Beobachtung weist darauf hin, dass die Zellen die Gradienten der Moleküle erfassen, um ihr Verhalten an die maximale Steigung der Gradienten anzupassen (siehe Abb.12.7a). Diese Fähigkeit zur Adaption wurde wie im Abschnitt 21.5 behandelt.

Um dieses Verhalten aufzuklären, beobachteten Block et al (1) die Rotation der (mit den Flagellen an Oberflächen fixierten) Bakterien. Betrachten wir zunächst, was wir nach der obigen Betrachtung mit einem Zweizustands-Modell erwarten. Kd sei die Dissoziationskonstante der Signalmoleküle ( $LaTeX: K_d \approx 10^{-4}$ M). Der Bruchteil besetzter Rezeptoren ist dann:

$LaTeX: P=\frac{P}{C+K_d}$

Man beachte, dass P gleich dem Verhältnis der Zeit im UZ ( $LaTeX: \tau_{UZ}$ ) zur Zeit im GUZ ( $LaTeX: \tau_{GUZ}$ ) ist. Die zeitliche Änderung der Besetzung ist daher:

$LaTeX: \frac{dP}{dt}=\frac{K_d}{(K_D+C)^2}\frac{dC}{dt}=\frac{CK_d}{(K_d+C)^2}\frac{d ln C}{dt}$

Das ist das oben erwähnte Ergebnis. Der erste Bruch auf der rechten Seite hat die Form einer Glockenkurve. Gl (2) zeigt ein interessantes Ergebnis: Falls die Antwort der Zelle tatsächlich proportional zu $LaTeX: \frac{dP}{dt}$ ist, so folgt sie dem bekannten Weber-Fechnerschen Gesetz. Ändert man nun die Konzentration C exponentiell mit der Zeit nach $LaTeX: C(t)= e^{\alpha t}$ ), so ist $LaTeX: \frac{dP}{dt}=\frac{dC}{dt}$ . 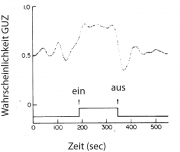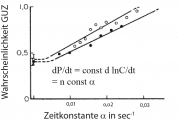Man erwartet also, dass beim Einschalten des Gradienten die Wahrscheinlichkeit des Zustands GUZ einen Sprung macht und dann im neuen Zustand verharrt, bis der Gradient wieder entfernt wird (s. Abb: A.21.3, links). Die Zeit die das Bakterium braucht, um sich auf den neuen Zustand einzustellen ist ein Maß für diejenige Zeit die das Bakterium braucht, um den Gradienten zu bestimmen. Ein weiteres wichtiges Ergebnis zeigt Abb. A. 21.3 (rechts). Die Wahrscheinlichkeit des Zustands GUZ steigt linear mit der Zeitkonstanten $LaTeX: \alpha$ der Konzentrationsrampe an.

[[File:21_2_neu.png|thumb|{(Abb. 4 in Referenz [1]). Links: Typische Antwort eines E.coli Bakteriums auf eine exponentiell ansteigende Konzentrationsrampe ( $LaTeX: \alpha = 0.015 s^{-1}$ ). Die Rampe wurde zur Zeit $LaTeX: t_1$ ein- und zu $LaTeX: t_2$ ausgeschaltet. Rechts: Messung der Wahrscheinlichkeit des Motors im GUZ Zustand als Funktion von $LaTeX: \alpha$

Vor den oben beschriebenen Experimenten mit den Konzentrationsrampen wurden die Verteilung der Verweilzeiten der Bakterien in den Zuständen ZU und GUZ bestimmt. Sie sind in Abb. A 21.2 dargestellt. Man sieht dass $LaTeX: \tau_{UZ}$ und $LaTeX: \tau_{GUZ}$ wieder exponentielles Verhalten zeigen. Die Verweilzeiten sind von der mittleren Konzentration C unabhängig, wie man es für ein adaptives System erwartet.

Verteilung der Verweilzeiten der Bakterien in den Zuständen UZ und GUZ. Die durchgezogenen Kurven sind reine Exponentialfunktionen.

Ein phänomenologisches Modell der Proportionalitätsreglers zur Adaption.

Ausgangspunkt ist die Beobachtung, dass die Bakterien zeitliche Änderungen der Konzentration und nicht diese selbst registrieren. Wir wollen nun die Frage beantworten, mit welchem Regelkreis Zellen zeitliche Änderungen von P beobachten können. Der Regelkreis muss also die zur Zeit t herrschende Besetzung der Rezeptoren mit der zur Zeit ( $LaTeX: t-\Delta t$ ) vergleichen. Ein einfacher Regelkreis der dies leistet ist der von Delbrück und Reichardt vorgeschlagene Proportionalitäts Regler . Er basiert auf der Annahme, dass sich eine interne Variable A, auf welche die Zelle eingestellt werden soll, mit der Rate (P-A) ändert. Man bezeichnet (P-A) als Fehlersignal. In unserem Fall ist A die in Gl (1) definierte Besetzung der Rezeptoren und P die Abweichung (bei der exponentiellen Änderung der Konzentration C der chemotaktischen Moleküle). Formal lässt sich das zeitliche Verhalten des Regelkreises durch die Gleichung:

$LaTeX: \frac{dA}{dt}=\frac{P-A}{\tau}$

beschreiben, wobei t die Ansprechzeit der Regelung ist. Ist A=P so wird $LaTeX: \frac{dA}{dt}= 0$ , d. h. das System ist voll adaptiert. Zur Veranschaulichung nehmen wir an die Besetzung der Rezeptoren werde mit der Rate $LaTeX: \alpha$ geändert. Die Größe A wird nach einiger Zeit auf den Wert $LaTeX: \alpha \tau$ einstellen. Die Zellen stellen sich also auf Änderungen $LaTeX: \Delta C$ ein, die in im Zeitbereich $LaTeX: \tau$ erfolgen.

Das Modell von Reichardt und Delbrück:

Das Modell beruht auf zwei Annahmen:

1. Die Antwort R des Reglers ist proportional zu Fehlersignal $LaTeX: R= g(P-A)$ (4) wobei g die Signalstärke festgelegt. A folgt P zeitlich verzögert gemäß: $LaTeX: \frac{dA}{dt}=\frac{P-A}{\tau}$ (5)

Man erhält A durch Lösen der inhomogenen Differentialgleichung (5). Danach kann man R(t) mit Hilfe von Gl (4) berechnen. Die Lösung der Gl (5) lautet:

$LaTeX: A(t)=\frac{e^{-\alpha t}}{\tau}\int_0^tP(t')e^{-\frac{t'}{\tau}}dt'$

Einsetzen liefert:

$LaTeX: R(t)=g\cdot (P(t)-\frac{1}{\tau}\int_0^tP(t')e^{-\frac{t-t'}{\tau}}dt')$

Der erste Term ist die momentane Besetzung der Rezeptoren. Der zweite Term ist der mit einem exponentiell zerfallenden Faktor gemittelte Wert von P und die Antwort des Regelkreises ist gleich der Differenz dieser Terme.

[1] S. Blocket al. (1983). J of Bacteriology 154: 312-323

Die Lösung der Aufgabe:

Nach der Diskussion in der Einleitung ist das Verhältnis der Verweilzeiten im GUZ und UZ durch die freien Energien der Zustände bestimmt. Wir können also die Besetzungszahlen mit Hilfe der Boltzmann Gleichung bestimmen. Die Bruchteile der Zeit im Zustand GUZ seien $LaTeX: r_1=0.01$ , $LaTeX: r_2=0.5$ . Daher wird $LaTeX: r_1 \propto exp(-\frac{\Delta G(GUZ)-\Delta G(UZ)}{RT})$ und $LaTeX: r_2 =0$ .Daher erhält man für die Energiedifferenz bei 37 ° C(=310 ° K):

$LaTeX: \frac{\Delta G(GUZ)-\Delta G(UZ)}{RT} \approx RT ln (50) \approx 3.9 RT$

(Zur Sicherheit berechnet man das Verhältnis $LaTeX: \frac{r_1}{r_2}=e^{-3.9}\approx 0.02$ )

Aufgabe 21.3:

Die diffusionsfreie (martensitische) Umwandlung der Flagellen

Vorbemerkung zu difusionsfreien strukurellen Änderungen:

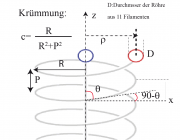
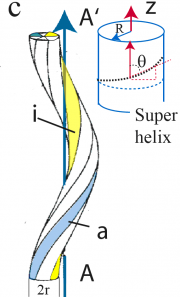
Strukturelle Umwandlungen in Festkörpern nennt man martensitisch wenn sie durch kooperative Umwandlungen (z.B. Scherung) und diffusionsfrei erfolgen. Sie sind dann besonders schnell. Ein technisch sehr wichtiges Beispiel ist Herstellung von Stählen durch schnelles Abkühlen aus einer Hochtemperaturphase $LaTeX: \alpha$ (Austenit) in eine Phase $LaTeX: \gamma$ . Die Umwandlung von einem kubisch flächenzentrierten in ein tetragonal raumzentriertes Gitter erfolgt durch eine kooperative Scherung des Gitters. Die Atome verschieben sich dabei nur um einen Bruchteil der Gitterkonstante. Im Fall der Flagellen wird die Umwandlung wahrscheinlich durch das Umklappen einiger der Filamente der Helix bewirkt. Dabei spielen die zunächst diskutierten besonderen topologischen Eigenschaften der Helix eine wesentliche Rolle. Eine knappe aber übersichtliche Darstellung der Eigenschaften der Schraubenlinie findet man in der Formelsammlung von Bronstein und Semendjajew:

Die Krümmung der Helix ist konstant (s. Abbildung). Die Konturlänge einer Ganghöhe $LaTeX: P = 2\pi p$ ist:

$LaTeX: S=2\pi\sqrt{R^2+p^2}$ (2)

Erinnerung an die Parameterdarstellung der Helix:

$LaTeX: x=R sin (\zeta)$ , $LaTeX: y=R cos (\zeta)$ , $LaTeX: z = \zeta t$ mit $LaTeX: \zeta=\frac{t}{\sqrt{R^2+P^2}}$ und $LaTeX: ds=dt\sqrt{R^2+p^2}$

In Abb. 21.7 wurde gezeigt, das eines der Filament an der Innenseite und eines an der Außenseite der durch die Protofilament gebildeten schraubenförmigen. Röhre verläuft. Damit die topologischen Bedingungen der Schraubenlinie erfüllt bleiben müssen die Konturlängen so eingestellt werden, dass sie dieselbe Ganghöhe besitzen. Um den Unterschied $LaTeX: \Delta S$ der Längen zu bestimmen benutzen wir Gl (2). Die Quadrate der Längen des äußeren ( $LaTeX: L_a$ ) und inneren Filaments ( $LaTeX: L_i$ ) sind nach Gl (2) :

$LaTeX: S_a^2=(4\pi R+2\pi D)^2+p^2$ $LaTeX: S_i^2=(4\pi R-2\pi D)^2+p^2$

Die Differenz ist:

$LaTeX: \Delta S \approx \sqrt{(2\pi R)^2+4\pi^2RD+p^2}-\sqrt{(\pi R)^2-4\pi^2RD+p^2} \approx \sqrt{(\pi R)^2+P^2}((1+2\frac{\pi^2RD}{(\pi R)^2+p^2})-(1-2\frac{\pi^2RD}{(\pi R)^2+p^2}))=\sqrt{\pi R^2+p^2}\frac{4\pi^2RD}{\pi R^2+p^2}$

Damit wird die relative Längendifferenz: $LaTeX: \Delta s= \frac{\Delta S}{S_a+S_i}=\frac{4\pi^2RD}{(2\pi)^2 (R^2+p^2)}=\frac{RD}{R^2+p^2}$

Das Ergebnis stimmt mit der Gleichung 21.5 überein, mit $LaTeX: p=2\pi P$ und $LaTeX: D=2r$ .

Aufgabe 21.4:

Messung der Drehmomente der Rotationsmotoren mittels magnetischer Pinzetten.

Es gibt verschiedene Möglichkeiten zur Messung der Drehmomente: Eingesetzt wurden vor allem zwei Methoden. Erstens, Rotierende elektrischen Felder, wobei die Kraft durch Maxwell-Wagner Polarisation erzeugt [1] wird, und zweitens, rotierende optische Fallen [2]. Der Vorteil der zweiten Methode ist die Möglichkeit, bis zu hohen Frequenzen von einigen 100Hz zu messen. Die Methode wurde von G. Fuhr et al. ausführlich beschrieben.

Grundlagen der Messung: Da die Reynoldszahl der Bakterien sehr klein ist (s. Kapitel 21 und 22) wird das angelegte Drehmoment M(t) durch folgende Faktoren bestimmt: Die Reibung mit dem Reibungskoeffizient $LaTeX: \zeta_r$ , das rücktreibende Moment aufgrund der Torsionssteifigkeit $LaTeX: k_t$ der Flagelle und die thermische Kraft $LaTeX: f_{th}(t)$ .

$LaTeX: -\zeta_r \Omega(t)=k_t \theta(t)+f_{th}(t)+M(t)$

In der Regel kann man die thermische Kraft vernachlässigen. Wenn die Drehmomente nicht zu groß sind, kann man auch die Torsionssteifigkeit ignorieren. Um noch das unbekannte rück treibende Moment durch die Reibung zu eliminieren geht man wie folgt vor [2]: Man beobachte die Rotation des an der Oberfläche befestigten Motors und misst die Rotationsgeschwindigkeit $LaTeX: \omega_0$ . Dann misst man diese ( $LaTeX: \omega_1$ ) bei eingeschaltetem äußerem Moment $LaTeX: M_{ex}$ . Nun erhöht man die Kraft bis der Motor im Schaft reißt und das Bakterium frei rotiert, d.h. die Geschwindigkeit $LaTeX: \omega_2$ durch den Reibungskoeffizienten $LaTeX: \zeta_r$ bestimmt ist. Die Geschwindigkeiten vor und nach dem Brechen der Verbindung zwischen Stator und Rotator sind gegeben durch:

$LaTeX: \omega_1=\frac{M_B(\omega_1)}{2\pi \zeta_r}$ und $LaTeX: \omega_2=\frac{M_{ex}+M_B}{2\pi \zeta_r}$

Nun bestimmt man die Differenz $LaTeX: \omega_2-\omega_1$ und bildet das Verhältnis:

$LaTeX: \frac{\omega_2-\omega_1}{\omega_1} = \frac{M_B(\omega_1)}{M_B(\omega_2)}$

$LaTeX: \omega_2-\omega_1$ ist proportional zum Moment des Motors bei der Geschwindigkeit $LaTeX: \omega_2$ Durch Division durch $LaTeX: \omega_1$ eliminiert man die unbekannte Reibung [2].

Messung mit magnetischen Pinzetten unter Benutzung super-paramagnetischer Kolloide:

Man benötigt dabei zylindrische Gebilde, um beim Einschalten des Magnetfeldes ein anisotropes magnetisches Moment zu erzeugen. Im rotierenden Magnetfeld dreht sich der Zylinder.

(1) S. Block et al. Nature 338; 514-518 (2) H. Berg and L. Turner (1993) Biophys, J 65: 2201-2215 (3) G Fuhr, R Glaser, and R Hagedorn (1986) Biophys J. February; 49: 395-402

Search

Navigation

SEARCH

TOOLBOX

LANGUAGES