Lösungen Kapitel 26

From BioPhy.de Wiki

Aufgabe 26.1:

Beweis der Gleichung 26.8b: $LaTeX: J(t) =\sum_i j_i (1-e^{t\frac{t}{\tau_i}})$

Man erinnere sich: J(t) ist die Kriechfunktion (oder Retardationsfunktion) der linearen Anordnung einer Parallelschaltung aus Feder und Dämpfung, die man auch Voigt Körper nennt. Jeder Voigt Körper der Anordnung in der Abbildung wird durch eine Kriechfunktion $LaTeX: J_i(t)$ bestimmt, die man mit der inhomogenen Differentialgleichung (DGl) der Form $LaTeX: \zeta _i \frac{dx_i}{dt}+k_ix=f_i$ bestimmen kann.

Schemazeichnung eines Voigt Körpers

Man löst zunächst die homogene Gleichung, welche offenbar die Form

$LaTeX: x_h(t)=Ce^{-\frac{k_i}{\zeta_i}t}$ (1)

hat. Nun wendet man die Variation der Konstante an, die darin besteht, C(t) zu einer zeitabhängigen Funktion zu machen. Setzt man $LaTeX: x_h(t)=C(t)e^{-\frac{k_i}{\zeta_i}t}$ in die DGL ein, so folgt $LaTeX: \zeta_i \frac{dC}{dt}-C(t)k_1+k_i C(t)=f_i e^{\frac{k_i}{\zeta_i}t}$ . Eine Lösung dieser Gleichung ist:

$LaTeX: C(t)=\frac{\zeta_i}{k_i}\frac{f_i}{\zeta_i} \int _0^tdte^{\frac{k_i}{\zeta_i}t}=\frac{f_i}{k_i} (e^{\frac{k_i}{\zeta_i}t}-1)$ (2)

Die gesamte Lösung der inhomogenen DGL erhält man durch Einsetzen der singulären Lösung für C(t) in Gl. 1. Mit der Definition $LaTeX: j_i=\frac{f_i}{k_i}$ folgt die zu beweisende Gleichung.

Zusatzaufgabe für Interessierte: Model von Festkörpern (engl: standard solid model von Zener und Kelvin).

Dieses lineare viskoelastische Modell wurde von Zener zur Beschreibung des Verhaltens von Festkörpern eingeführt, insbesondere, um deren Kriechverhalten und die Spannungsrelaxation zu beschreiben. Das Kriechen spielt eine wichtige Rolle bei der plastischen Verformung von Metallen und Holz, sowie bei Knochenbrüchen und die Messung und quantitative Charakterisierung ihrer viskoelastischen Eigenschaften ist von großem technischen Interesse. In Metallen ist das Kriechen durch das gegenseitige Gleiten des Materials entlang von Kristallebenen bestimmt, während in Holz die Fasern aneinander gleiten.

Das Zener Modell besteht aus einer parallelen Anordnung eines Maxwell Modells und einer zweiten Feder (s. Abbildung 1). Das Modell wurde tatsächlich erstmals von Kelvin zur Beschreibung des mechanischen Verhaltens des Äthers eingeführt. In den letzten Jahren hat sich gezeigt, dass das Kelvin Modell die einfachste Beschreibung der viskoelastischen Deformation von Zellmembranen und Zellen durch Punktkräfte [1],[2] ermöglicht. Schließlich haben wir in Kapitel 32 gesehen, dass das Modell eine wichtige Rolle zur Beschreibung der Mechanik der Haarzellen (OHZ) spielt. Wir wollen in dieser Zusatzaufgabe die Lösung der viskoelastischen Antwort des Zener/Kelvin-Modells auf einen Kraftimpuls beschreiben.

Die Bewegungsgleichung für eine Parallelschaltung aus einem Maxwell-Körper ( $LaTeX: \mu_i , \zeta_1)$ und einer zweiten Feder mit dem Modul $LaTeX: \mu_2$ kann man leicht ableiten, wenn man berücksichtigt, dass die gesamte äußere Kraft $LaTeX: F_0$ gleich der Summe der Kräfte in den beiden Zweigen ist, und dass die Dehnung des Maxwellkörpers aus zwei Beiträgen besteht:

$LaTeX: u=u_1+u_1'$ (1a)

$LaTeX: F=F_0 + F_1$ (1b)

Die Kraft im Zweig 1 kann auf zwei Weisen ausgedrückt werden:

$LaTeX: \zeta_1 \frac{du_1}{dt}$ oder $LaTeX: \zeta_1 \frac{du_1}{dt}-\mu_1 u'_1=0$ (1c)

Die gesamte statische Kraft ist gegeben durch:

$LaTeX: F=(\mu_0u+\mu_1u_1')=(\mu_0+\mu_1)u-\mu_1u_1$ (1)

Die aus dem statischen und dynamischen Anteil bestehende Gleichgewichtsbedingung hat dann die Form (s. auch Kapitel 26.1):

$LaTeX: F+\frac{\zeta_1}{\mu_1}\frac{d}{dt}F=(\mu_1+\mu_2)u-\mu_1u_1+\frac{\zeta_1}{\mu_1}((\mu_1+\mu_2)\frac{du}{dt})$ (2)

Wir können nun den letzten Term ersetzen durch: $LaTeX: \zeta_1\frac{du_1}{dt}=\mu_1u_1'$ und $LaTeX: u_1'$ durch $LaTeX: u-u'$ und erhalten: $LaTeX: F+\frac{\zeta_1}{\mu_1}\frac{d}{dt}F=\mu_2u+\frac{\zeta_1}{\mu_1}((\mu_1+\mu_2)\frac{du}{dt})$ (3)

Unmittelbar nach dem Kraftstoß dominieren die Terme der zeitlichen Ableitung und es wird:

$LaTeX: u(0)=\frac{F}{\mu_1 + \mu_2}$ (4)

Der Körper verhält sich elastisch und die Amplitude der Auslenkung liefert die den gesamten elastischen Modul des Kelvin Körpers. Für $LaTeX: t \rightarrow \infty$ wird die Auslenkung durch die maximale Amplitude bestimmt: $LaTeX: u_{max}=\frac{F}{\mu_2}$

Das zeitliche Verhalten für lange Zeiten wird durch die

$LaTeX: u_{ij}(t)=\frac{1}{\mu_2}(1-(1-\frac{\tau_1}{\tau_2})e^{-\frac{t}{\tau_1}}) \sigma_{ij}$

, wobei

$LaTeX: \tau_1 = \frac{\zeta_1}{\mu_1}$ ; $LaTeX: \tau_2=(\frac{1}{\mu_1}+\frac{1}{\mu_2}) \zeta_1$

ist, gegeben.

Aufgabe 26.2:

Welche Form hat die viskoelastische Kriechfunktion (Antwort auf einen Kraftsprung) eines Maxwell Modells und eines Voigt Modells?

Denken Sie daran, dass beim Maxwell Modell die Deformation gleich der Summe der Deformationen der Einzelkomponenten ist.

Für Hilfe siehe Y. C. Fung: 'Biomechanik', Springer Verlag

Ein Wort zur Vorsicht bei Impulsexperimenten. Ein Vorteil der viskoelastischen Impedanzspektroskopie ist die Möglichkeit Impulsfolgen anzulegen, um die Meßgenauigkeit zu verbessern oder um die Wirkung von Wirkstoffen oder Hormonen als Funktion der Zeit zu untersuchen (wie im Fall der Experimente von Feneberg et al.[1]). Dabei muss man jedoch darauf achten, dass die Zeiten zwischen den Kraftimpulsen lang genug sind, da sonst nichtlineare Effekte auftreten können.

Um diese zu sehen, betrachten wir ein typisches Dehnungs-Relaxations-experiment. Der Kraftsprung der Amplitude $LaTeX: F_0$ am Beginn des Impulses beschreiben wir als Heavyside Funktion $LaTeX: \theta(t-t_0)$ mit folgenden Werten: $LaTeX: \theta(t-t_0)=0$ für $LaTeX: t < t_0$ und $LaTeX: \theta(t-t_0)=1$ für $LaTeX: t \leq 0$ . Die Auslenkung u(t) hat die Form:

$LaTeX: u(t)=F_0\int_{-\infty}^t j(t-t')\delta(t-t_0)dt'=F_0j(t-t_0)$ (1)

Dabei ist $LaTeX: \delta (t-t')$ die Kronecker Deltafunktion, die gleich der ersten zeitlichen Ableitung der Heavyside Funktion ist.

Betrachten wir nun eine Folge von Kraftimpulsen $LaTeX: F_0, F_1 ... F_N$ : Man kann diese als Serie von Heavyside-Funktionen darstellen, welche die Kräfte ein und ausschalten. Betrachten wir einen Impuls der zur Zeit $LaTeX: t_0$ angelegt und zur Zeit $LaTeX: t_0+T$ abgeschaltet wird. Das Abschalten erfolgt mathematisch durch Anlegen eines Stufenfunktion mit negativer Amplitude: $LaTeX: -F_0$ . Und die gesamte Deformation des Körpers hat dann für den Impuls der zur Zeit t=0 angelegt wird die Form:

$LaTeX: u(t)=F_0(j(t-0)-j(t-T))$ (2)

Offenbar ist die Deformation nur reversibel (u(t) =0), wenn T größer ist als die längste Relaxationszeit des Prozesses.

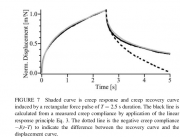
Wir betrachten im Folgenden ein Beispiel aus der Doktorarbeit von Wofgang Feneberg [1]. (Abb: 7 in [1]). Die graue Kurve zeigt die durch einen Kraftimpuls von 2.5 sec induziert Kriechfunktion. Die schwarze Kurve wurde mit Hilfe der linearen Antwortfunktion Gl(2) berechnet. Die Kurven stimmen hervorragend überein. Sie gehen jedoch nicht auf null zurück, da die Impulsdauer kleiner ist, als die Relaxationszeit ( $LaTeX: T < t_R$ ) des Prozesses. Wäre $LaTeX: T>t_R$ , so würde die Relaxation durch die gestrichelte Kurve realisiert.

Die wichtigste Botschaft der obigen Betrachtung ist, dass man bei der Interpretation der Kriechfunktionen vorsichtig sein muß. Bei einer naiven Betrachtung würde man aus den experimentellen Kurve in Abb. 7 schließen, dass die viskoelastische Antwort nichtlinear ist und die Relaxation der Deformation durch andere dissipative Prozesse bestimmt als die der Deformation.

Referenzen:

1 Feneberg, W., Aepfelbacher ,M., Sackmann, E.(2004) Microviscoelasticity of the Apical Cell Surface of Human Umbilical Vein Endothelial Cells (HUVEC) within Confluent Monolayers. Biophys, J 87: 1338-1350.

2 Bausch, A., Moeller, W. Sackmann, E. (1999). Measurement of local viscoelasticity and forces in living cells by magnetic tweezers. Biophys. J. 76:573 - 579.

Aufgabe 26.3:

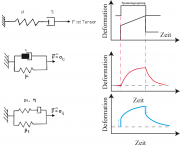
Die Charakteristischen Formen der viskoelastischen Antwort des Maxwell-, Voigt- und Kelvin-Modells.

Jedes der spezifischen Modelle hat einen charakteristischen Verlauf der Kriechfunktion, den man sich bei Betrachtung des mechanischen Äquivalenzkreises leicht selbst überlegen kann:

Maxwellmodell: Da im Maxwellmodell die Feder und das Dämpfungsglied unabhängig voneinander deformiert werden, entsteht erst ein elastischer Deformationssprung. Danach dehnt sich der Körper kontinuierlich mit konstanter Geschwindigkeit.

Voigtmodell: In diesem Fall kann sich die Feder nur retardiert dehnen. Ein Beispiel wäre ein vernetztes Polymer (Gel) oberhalb des Glaspunktes. Bei Anlegen eines Kraftimpulses fängt das Gel an zu fließen, indem die gefalteten Polymermoleküle gestreckt werden. Diese Entfaltung der Polymerketten erfolgt mit einer Folge von Ansprechzeiten, z. B. den Rouse-Relaxationszeiten im Fall synthetischer Polymere oder den in Kapitel 25.5 abgeleiteten Relaxationszeiten im Fall der Aktinfilamente.

Kelvin/Zener Modell: In diesem Fall können sich die beiden Federn gleichzeitig unendlich schnell dehnen und zwar um den Betrag $LaTeX: \delta u = \frac{f}{\mu_1+\mu_2}$ . Danach erfolgt die weitere Dehnung verzögert mit einer effektiven Relaxationzeit von:

$LaTeX: \tau=\eta(\frac{1}{\mu_1}+\frac{1}{\mu_2})$

Das Modell beschreibt das Deformationsverhalten der Polymere unterhalb des Glasübergangs.

Search

Navigation

SEARCH

TOOLBOX

LANGUAGES

Lösungen Kapitel 26

From BioPhy.de Wiki

Aufgabe 26.1:

Aufgabe 26.2:

Aufgabe 26.3:

Toolbox