Lösungen Kapitel 13

From BioPhy.de Wiki

Aufgabe 13.1:

Van der Waals-Kontraktion versus entropische Abstoßung.

Vorbemerkung: Wir betrachten als Beispiel die Van der Waals-Wechselwirkung zwischen einer Lipidschicht (Dicke $LaTeX: d_m$ ) und einer Glasoberfläche. Diese ist:

$LaTeX: V(h)= \frac{H_{MG}}{12 \pi}[\frac{1}{h^2}-\frac{1}{(h+d_m}^2]$

Man erhält diese Gleichung, wenn man die Wechselwirkungen zwischen der Glasoberfläche und einer Halbebene aus Lipid im Anstand h bzw. aus Wasser im Abstand (h+ $LaTeX: d_m$ ) betrachtet und berücksichtigt, dass die Wechselwirkung zwischen zwei Halbebenen $LaTeX: \frac{H}{12 \pi h^2}$ ist. Entsprechend gilt für zwei isolierte Membranen:

$LaTeX: V(h) = \frac{H_{MM}}{12 \pi}[\frac{1}{(h+2d_m)^2}-\frac{1}{h^2}+\frac{2}{(h+d_m)^2}]$ (1)

mit angeregten Biegefluktuationen. Es ist $LaTeX: H_{MG} \approx 8.0 \cdot 10^{-21}J$ und $LaTeX: H_{MM} \approx 5 \cdot 10^{-21} J$ , d.h. die Werte sind ähnlich groß.

Da die Ondulationskräfte Abstoßungsdrücke erzeugen (und nicht als wirkliche Potentiale zu betrachten sind) ist es sinnvoller, Kräfte pro Fläche zu betrachten. Für den hier betrachteten Fall der Wechselwirkung der Membran mit Glas gilt:

$LaTeX: f(h)=\frac{H_{MG}}{6\pi}[\frac{1}{h^3}-\frac{1}{(h+d_m)^3}]\approx \frac{3k_BT}{2\pi} \frac{1}{h^3}(1-3\frac{d_m}{h})$ (2)

Die Näherung gilt natürlich nur für $LaTeX: d_m$ << h. Die Gleichung für den Ondulationsdruck lautet (Kapitel 11.5.3): $LaTeX: p_{disj}\char`\~ \frac{(k_BT)^2}{16 \kappa h^3}\char`\~ \frac{k_BT}{160 h^3}$ , wobei die rechte Gleichung für Lipidmembranen mit $LaTeX: \kappa \char`\~ 10 k_BT$ gilt (s. Tabelle 11.1).

Der Vergleich der Gleichungen zeigt, dass der repulsive Ondulationsdruck vergleichbar wird mit der Van der Waals Anziehung, falls $LaTeX: h \approx \frac{d_m}{3} \approx 12 nm$ . Das entspricht in etwa der Länge mit der Kopfgruppen vieler Membranproteine, die aus der Membran herausragen.

Ergänzungen zur Wechselwirkung zwischen freien Membranen:

Die Van der Waals-Attraktion zweier freier Membranen ist nach Gl (1) von der Größe $LaTeX: f(h) \approx \frac{H_{MM}}{6\pi}\frac{6 d_m}{h}$ . Mit $LaTeX: H_{MM} \approx k_BT$ folgt, dass die Kräfte vergleichbar sind, falls $LaTeX: h \approx 50 d_m$ \char`\~ $LaTeX: 200nm$ . Die Ondulationskräfte dominieren die Wechselwirkung also bei sehr viel größeren Abständen. Dies hat interessante Konsequenzen für die Wechselwirkung zwischen nicht-sphärischen intrazellulären Organellen, wie dem ER oder den Endosomen. Die Ondulationen verhindern das Verkleben der Organellen, falls sie nicht durch spezifische Kräfte zwischen Oberflächen-Rezeptoren erzwungen wird. Die Abstoßung zwischen den Organellen kann auch durch laterale Spannungen getriggert werden.

Aufgabe 13.2:

Herstellung festkörpergestützter Membranen durch Vesikelfusion auf Oberflächen.

Motivation: Seit den ersten Versuchen zur Herstellung Festkörpergestützter Lipidfilme vor rund 20 Jahren (s. McConnell und Tamm 1984; Review: Sackmann 1996), gewinnen diese Modellmembranen zunehmend an Bedeutung; zur Herstellung von biologisch aktiven Grenzschichten auf Halbleiterbauelementen (zum Aufbau von Biosensoren) oder zum Aufbau von Modellen der Zelloberfläche. Es eröffnete sich dadurch ein neues Gebiet zwischen Festkörperphysik und Biophysik. Es gibt zahlreiche Methoden zur Herstellung solcher Filme.

a) Wir betrachten hier die häufig verwendete Vesikel-Fusion bei hohen Adhäsionsenergien $LaTeX: W_{ad}$ . Dabei nehmen die Vesikel die Form einer Kugelkappe (s Abb. A13.1b). Man kann in diesem Fall immer noch einen effektiven Kontaktwinkel $LaTeX: \theta_{eff}$ definieren und die Young-Gleichung (Gl.13.2) anwenden (s. [Lipowsky und Seifert 1995]): $LaTeX: W_{ad}=\Sigma(1-cos\theta_{eff})$ . Wie wir in Kapitel 12 lernten, platzen die Vesikel (der entspannten Oberfläche $LaTeX: A_0$ ) durch Porenbildung an der Spitze bei einer kritischen Dehnung von $LaTeX: a*=\frac{A_0 - A}{A_0 } \geq a* \approx 0.03$ auf. Für Vesikel aus SOPC (bzw: 1:1 SOPC/Cholesterol Mischungen) ist der Kompressionsmodul nach Tabelle 11.1 $LaTeX: K \approx 200 \frac{mN}{m}$ (bzw. $LaTeX: K \approx 1700 \frac{mN}{m}$ ) und die kritische Spannung ist daher $LaTeX: \Sigma * = Ka* \approx 6\frac{mN}{m}$ (bzw. $LaTeX: 50 \frac{mN}{m}$ ). Wenn die Vesikel zu Beginn eine große Überschussfläche besitzen, nehmen sie vor dem Platzen eine pfannkuchenartige Form an, d.h. $LaTeX: \theta_{eff}$ \char`\~ $LaTeX: \pi$ und $LaTeX: \Sigma$ \char`\~ $LaTeX: \frac{W_{ad}}{2}$ . Man benötigt also Adhäsionsenergien von W\char`\~ 12 $LaTeX: \frac{mJ}{m^2}$ (bzw. 100 $LaTeX: \frac{mJ}{m^2}$ ). Abb. 13A.1C zeigt als Beispiel die Spreitung eines Vesikels auf F. Gleichzeitig sieht man ein kugelkappenförmiges Vesikel. Durch Aufnahme des Spreitens mittels RICM kann man sowohl die Dicke des fusionierten Bilayers und $LaTeX: \theta_{eff}$ messen.

Festkörpergestützte Membranen. a) Aufbau von Biosensoren und Modellen der Zelloberfläche durch Trennung der Membranen von der Proteine denaturierenden Festkörperoberfläche durch Polymerkissen. b) Herstellung elektrisch isolierender Membranen. Links: Übertragung von Doppelschichten. c) Spreitung eines geplatzten Vesikels (oben im Bild) und einer Kugelkappe (unteren im s Bild) nach [J. Rädler et al Langmuir 11, 4539,(1995)].

Ergänzung zu Frage a:

Wir haben oben die Krümmungsenergie vernachlässigt. Für kleine Vesikel gilt dies nicht mehr. Für diese hängt das Verhalten von der Bilanz des Gewinns an Biegenergie und des Aufwands an Randenergie ab. Diese ist bestimmt durch die Gleichung: $LaTeX: \Delta G = -4 \pi wR^2 + 2\pi R\Gamma_R$ , wobei w die Adhäsionsenergie und $LaTeX: \Gamma_R$ die in Aufgabe 12.5 definierte Randenergie der beim Platzen entstehenden Scheibe ist. (Sie hat einen Wert von G $LaTeX: \approx$ 25 pN. In erster Näherung erwartet man, dass die Vesikel instabil werden, wenn der Energieaufwand $LaTeX: \Delta G$ ein Minimum ist. Diese Bedingung bestimmt den minimalen Radius $LaTeX: R_{min}$ , die ein Vesikel haben muss, um zu platzen (falls keine Detergenzien in der Membran gelöst sind). Es wird $LaTeX: R_min = \frac{R}{2w}$ . Für typische Werte von $LaTeX: 10^{-3} <w <10^{-2} \frac{mN}{m}$ variiert $LaTeX: R_{min}$ von 1-10 $LaTeX: \mu m$ . Eine genauere Theorie findet man in den unten zitierten Arbeiten von Lipowsky und Seifert.

Frage b: Nach dem in Teil a beschriebenen Modell ist die kritische Spannung $LaTeX: \Gamma * =K a*$ . Für SOPC ist K=200, und a*=0.03. Die minimale Flächendichte der Biotine ist: $LaTeX: n = \frac{N}{A} \approx 5 1016 pro m^2$ .

Zusatzfrage: Zur Beantwortung dieser Frage kann von Gl 13.8 in Kapitel 13.3 ausgehen. Eine detaillierter Betrachtung findet man in der Arbeit von Bruinsma et al. Phys. Rev. E.61: 4253 (2000) Gl.3.10. Das einfachste Verfahren zur Kontrolle der Adhäsionsenergie W ist die Dotierung der Vesikel mit polymere Kopfgruppen tragenden Lipide (z.B. aus Polyethylenoxid). Nach Gleichung 13.8 reduziert der durch Puffermoleküle der Konzentration $LaTeX: c-P$ erzeugte osmotische Druck die Adhäsionsstärke um $LaTeX: k_BT c_P$ . Es reichen wenige Mol\

Praktische Hinweise: Einzelne Doppelschichten spreiten auf Glas (und auf mit dünne Filmen aus Hyaluronsäure) bedeckten Substraten spontan, indem man einen Klumpen aus Lipid auf das Substrat deponiert und mit Wasser bedeckt. Es handelt sich dabei um ein schönes Beispiel des Wachstums zweidimensionaler Strukturen auf rauen Oberflächen, die durch die berühmte Kadar-Parisi-Zhang Gleichung (KPZ-Gleichung) beschrieben wird [Rädler].

Referenzen: H. M McConnell L.Tamm Proc. Natl. Acad. Sci. 81:324 (1984) E. Sackmann Supported Membranes: Scientific and Practical Applications. Science (1996) 271, 43-48. E. Sackmann , M. Tanaka M. Trends Biotechnol. 18:58-64.(2000) S. Seiffert und R. Lipowsky Handbook of Biological Physics, Vol 1B (1995). S. Seiffert und R. Lipowsky Mol. Cryst. Liquid Cryst. 202: 17-25 (1991).

Aufgabe 13.3:

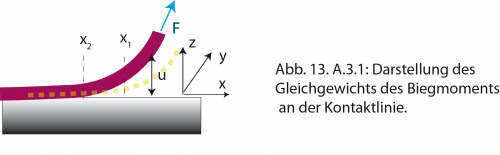
Das Momentengleichgewicht bestimmt den Kontaktwinkel.

Die Form adhärierender Schalen in der Nähe der Substratoberfläche ist durch zwei Randbedingungen (erster Ordnung) bestimmt: Eine ist das in Kapitel 13 diskutierte Gleichgewicht der Oberflächenspannungen. Die zweite ist das Gleichgewicht der Biegemoment an der Randlinie. Wenn die Randlinie jedoch scharfe Kanten aufweist, wie bei der Bildung stark haftender Mikrodomänen, so muss auch noch eine Randbedingung berücksichtigt werden, welche das Gleichgewicht der Gradienten der Biegemomente berücksichtigt. Eine sehr ausführliche Diskussion dieser Randbedingung findet man in §11 des Lehrbuchs von Landau und Lifshitz (Band VII Elastizitätstheorie). Die Anwendung auf Membranen findet man in Guttenberg et al. Langmuir. 16 8984 (2000).

Zur Lösung des Problems betrachten wir die folgende Skizze:

Das durch die nach oben gerichtete Kraft erzeugte Drehmoment bestimmt die Krümmung $LaTeX: C=\frac{\partial^2 u}{\partial x^2}$ an der Kontaktlinie, wobei u die Auslenkung in z-Richtung ist. Nach Gl 11.4 gilt $LaTeX: C=\frac{M}{\kappa}$ . Durch Anlegen eines Zusatzmoments wird Kontaktfläche um $LaTeX: \delta u$ nach oben und um $LaTeX: \delta x$ nach links verschoben. Dabei wird die Fläche $LaTeX: \delta x$ pro Einheitslänge in Richtung der y-Achse freigelegt.

Die Deformation kostet folgende mechanische Arbeit

$LaTeX: \delta g =M \frac{\partial \delta u }{\partial x}=M \frac{\partial ^2 u}{\partial x^2} \partial x$ (1)

Diese Gleichung folgt aus der Betrachtung der Dimension von $LaTeX: \delta g$ die [Arbeit pro Länge] oder [N] ist. $LaTeX: \delta g \propto \frac{\partial \delta u}{\delta x}$ folgt auch aus der Überlegung, dass $LaTeX: \frac{\partial \delta u }{\partial x}$ gleich dem Winkelinkrement $LaTeX: \delta \Phi$ ist, um das die Tangente an die Kontur entgegen dem Uhrzeigersinn gedreht wird und die Arbeit pro Länge gleich $LaTeX: M \delta \Phi$ ist. Andererseits ist $LaTeX: \delta u= \frac{\partial u}{\partial x}\partial x$ , womit die rechte Seite von Gl (1) begründet ist. Nun müssen wir noch beachten, dass wir durch Verringerung der Kontaktfläche um $LaTeX: \delta x$ zweimal die Adhäsionsenergie $LaTeX: W \delta x$ verlieren (wobei W die Adhäsionsenergie pro Fläche ist). Damit ist Gl. 13.3 bewiesen.