Lösungen Kapitel 19

From BioPhy.de Wiki

Aufgabe 19.1:

Krafterzeugung durch optische Pinzetten.

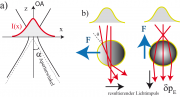
Optische Pinzetten gehören heutzutage zur Standardausrüstung eines Biophysiklabors. Es ist daher lehrreich und wichtig, sich mit den physikalischen Grundlagen der Kraftentstehung zu befassen. Je nach dem Durchmesser d der zu untersuchenden Partikel hat man es mit zwei Situationen zu tun: d klein gegen die Wellenlänge $LaTeX: \lambda$ und d ~ $LaTeX: \lambda$ .

Für $LaTeX: d << \lambda$ hat man es wie bei der Rayleigh Streuung mit der Wechselwirkung eines polarisierbaren Teilchen (Polarisierbarkeit $LaTeX: \alpha$ ) mit dem elektrischen Feld E( $LaTeX: \alpha$ ) des Lichtes zu tun (s. Abbildung 19A.1. 1a).

Man muss dabei beachten, dass die Polarisierbarkeit durch die Clausius-Massotti Beziehung mit den Dielektrizitätskonstanten ( $LaTeX: \epsilon_1$ und $LaTeX: \epsilon_2$ ) Brechungsindizes ( $LaTeX: n_1$ und $LaTeX: n_2$ ) der Materialien verknüpft ist:

$LaTeX: P'=\frac{\epsilon_1 - \epsilon_2}{\epsilon_1+2\epsilon_2}\frac{M}{\rho}=\alpha \frac{N_A}{3\epsilon_0}$ (1)

M ist die Molmasse ( $LaTeX: \frac{kg}{M}$ ) und $LaTeX: \rho$ ist die Dichte ( $LaTeX: \frac{kg}{m^3}$ ). P hat also die Dimension Molvolumen. Häufig wird $LaTeX: \epsilon_2=1$ (was nur für Partikel in Luft als eine gute Näherung gilt).

Im elektrischen Feld des Licht wir das im Teilchen induzierte Dipolmoment $LaTeX: \vec{M}=n\alpha \vec{E}$ wobei n die Dichte der Dipole im betrachteten Partikel ist, das als isotrop betrachtet wird. Die Kraft auf das Teilchen im inhomogenen Feld des fokussierten Lichts ist dann:

$LaTeX: \vec{F}=\vec{M}\nabla{}|E|$

Abb 19.A.1: Zur Demonstration der Kraft auf die Partikel der optischen Pinzette

Für $LaTeX: \lambda <<d$ erhält man die Kraft auf das Teilchen durch Betrachtung des Strahlungsdruck der Lichtstrahlen. Hier ist es für Nichtspezialisten ausreichend, sich auf die geometrische Betrachtung anhand der rechten Abbildung zu beschränken.

Die Abbildung 19A.1 zeigt, dass die Richtung der Kraft und die Bedingungen unter denen die Teilchen im Fokus gefangen werden in beiden Betrachtungen äquivalent sind. Die Berechnung der absoluten Kräfte auf das Teilchen ist schwierig und nicht nötig, da man im Experiment die Kraft bestimmt, in dem man die die Reduktion der Brownschen Bewegung im Kraftfeld des Lichtes misst. Dabei nimmt man an, dass man das Kraftfeld durch ein harmonisches Potential ersetzen kann ( $LaTeX: V=k \frac{x^2}{2}$ ). Dieser Fall wurde mehrfach im Buch diskutiert, wobei gezeigt wurde, dass das mittlere Verschiebungsquadrat des Partikels in Richtung senkrecht zur optischen Achse gegeben ist durch $LaTeX: <|x(0)^2|> =\frac{k_BT}{k}$ .

Zusatzfrage. Wie ändert sich die Situation, wenn der Brechungsindex des Partikels kleiner ist, als der des umgebenden Mediums (Situation einer Luftblase in Wasser). Nach der Clausius Masotti Bezeihung (1) ändert sich das Vorzeichen des induzierten Dipolmoments und das Partikel wird aus der Falle entfernt. Man kann sich dies durch Betrachtung des Lichtdruckes klar machen.

Aufgabe 19.2:

Der Strahlungsdruck des Lasers.

James Clerk Maxwell zeigte schon 1873, dass elektromagnetische Wellen einen Druck auf Körper ausüben können.

Ein Photon der Frequenz $LaTeX: \nu$ transportiert die Energie $LaTeX: E = h\nu$ . Es besitzt die Masse $LaTeX: m = \frac{h \nu}{c^2}$ und damit den Impuls $LaTeX: p=\frac{h\nu}{c}=\hbar k$ . Treffen in der Zeit dt dN Photonen auf eine Oberfläche, so ist der Impulsübertrag pro Zeiteinheit (d.h. die Kraft) $LaTeX: \frac{dp}{dt}=\frac{h \nu}{c}\frac{dN}{dt}$ , falls alles Licht absorbiert wird. Auf eine gegen den Lichtstrahl um den Winkel $LaTeX: \theta$ geneigte Fläche wird der Strahlungsdruck $LaTeX: P_i=\frac{dp}{dt}=\frac{h \nu}{c \cdot dA \cdot cos(\theta)}\frac{dN}{dt}$ ausgeübt. Die Größe $LaTeX: \Phi$ (Dimension $LaTeX: \frac{J}{s} =W$ ) wird als Strahlungsstrom bezeichnet und die Größe $LaTeX: E_i$ als Bestrahlungsstärke (engl. energy flux) Dimension $LaTeX: [E_s]=\frac{Js}{m^2}$ und hat die Dimension der Intensität. Daher wird der Strahlungsdruck $LaTeX: P_s=\frac{E}{c}$ .

Das Ergebnis der Rechnung ist: Der Strahlungsdruck auf das vollkommen absorbierende Partikel ist ungefähr gleich der Energiedichte der einfallenden Strahlung des Laser. Man beachte: Bei totaler Reflexion ist der Strahlungsdruck doppelt so groß.

Anwendung: Wir betrachten einen Laser mit 1 W Strahlungsleistung und 10 $LaTeX: \mu m$ Strahldurchmesser. Die Bestrahlungsstärke ist: $LaTeX: E_s \approx 10^{10} \frac{W}{m^2}$ . Der Strahlungsdruck ist: $LaTeX: P_s \approx 50 Pa (= 3 10^{-3} atm)$ . Die Kraft auf ein 1 $LaTeX: \mu m$ Partikel ist: für 100 % Reflektivität (r=1): 10pN; für Gold (r=0.75): 9 pN; und für Glas (r = 0.04): 0.3 pN. Zum Vergleich: Der Strahlungsdruck der Sonne ( $LaTeX: E_s \approx 10^3 \frac{W}{m^2}$ ) ist $LaTeX: P_s \approx 4.5 \mu Pa$ .

Aufgabe 19.3:

Kraftmessung mit magnetischen Pinzetten.

Die Kraftmessung mit magnetischen Partikeln (Pinzetten) hat den Vorteil, dass sie völlig berührungsfrei und störungsfrei ist.

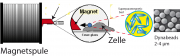
Superparagnetismus: Die magnetischen Pinzetten (MPZ) bestehen aus Polymerkügelchen mit eingebauten ferromagnetischen Nanopartikeln aus $LaTeX: Fe_2O_3$ (s. Abbildung 19A.3.1). Letztere sind kleiner als die Weißschen Bezirke (Durchmesser je nach Material 3-50 nm). Sie sind daher nicht ferromagnetisch und besitzen keine Koerzitivkraft. In Abwesenheit des Feldes klappen die Momente durch thermische Fluktuation ständig um (mit Neel-Relaxationszeiten $LaTeX: t_N<10^{-9} s$ ) und die MPZ sind nicht magnetisiert. Im Magnetfeld richten sich die Nanomagnete aus und es entstehen große magnetische Momente. Sie verhalten sich also wie Paramagnete und man nennt sie daher super-paramagnetisch. Die magnetische Suszeptibilität der Pinzetten ist wie bei normalen Paramagneten durch eine Langevin Funktion bestimmt. Die Kraft auf die Pinzetten ist daher bestimmt durch:

$LaTeX: F=(\vec{M}(B)\nabla{})\vec{B}$ (1)

$LaTeX: \mu_0$ ist die magnetische Permeabilität gemessen in $LaTeX: \frac{N}{A^2}$ ( $LaTeX: 4 \pi \cdot 10^{-7} \frac{N}{A^2}$ ). M ist das vom magnetischen Fluss abhängige magnetische Moment (Dimension [ $LaTeX: A m^2$ ]) und B ist der magnetische Fluss (Dimension (V $LaTeX: \frac{s}{m^2}$ oder Tesla). Das Verhalten ist sehr kompliziert. In der Praxis umgeht man das Problem, indem man die Kraft als Funktion des Gradienten des magnetischen Flusses (oder einfach des Spulenstroms) bestimmt (s. beispielsweise Ziemann et al. Biophys. J 66, 2210,(1994)). Man misst dazu die Geschwindigkeit der MPZ in Wasser-Glyzerin-Mischungen. Den Reibungskoeffizienten kann man, wie im Fall der optischen Pinzetten in Aufgabe 19.1) durch Analyse der Brownschen Bewegung messen.

Aufgabe 19.A.3.1 Schematische Darstellung der Kraft-Messung mit magnetischen Pinzetten. Man kann die Spule auch durch sehr spitze magnetische Nadeln erzeugen, die mit Mikromanipulatoren an den Ort der MPZ bewegt wird.

Anwendung: Messung der Entbindungskraft von auf Aktinfilamenten laufenden Myosin V-Motoren. Abb. 19A.3.2 zeigt das Prinzip der Methode.

Abb 19.A.3.2 a) Anordnung zur Messung der Entbindungskraft von auf Aktinfilamenten laufenden MyoV-Motoren. Mit der Anordnung können 100pN erreicht werden. b) Beobachtung der Entbindung durch Analyse der Breite des Beugungsscheibchens des fluoreszierenden MPZ, deren Intensitätsverteilung man als Gaussfunktion darstellen kann (Höhenauflösung 7 nm).

Zum Experiment: Man fixiert fluoreszierende Aktinfilamente auf einer Glasplatte und koppelt die Myosin V Motoren auf den MPZ, der ebenfalls fluoresziert. Der Strom wird durch einen Funktionsgenerator gesteuert, mit dem man die zeitliche Änderung der Kraft variieren kann, um die Entbindungskraft als Funktion der Kraftrate zu messen. Die Methode zur Beobachtung der Entbindung wird unten beschrieben.

Messung des Abstandes zwischen dem MPZ und dem Aktinfilament: Hier nutzt man die Änderung des Beugungsbildes der fluoreszierenden Sonde aus, die durch dessen Entfernung aus der Fokusebene auftritt. Wie im Kapitel 37 gezeigt wird, kann man die Intensitätsverteilung als Gaussfunktion darstellen. Deren Breite nimmt zu, wenn die Sonde aus dem Fokus entfernt wird (wie in Abb. 19.A.3.2b gezeigt wird). Man kann mit dieser Methode Höhenauflösungen von 7 nm erreichen. (siehe A. Roth Doktorarbeit Technische Universität München 2006 (siehe http://mediatum2.ub.tum.de/node, Rubrik Fakultät für Physik))

Aufgabe 19.4:

Beweis der Gleichung 19.3. Analyse der Kinetik gekoppelter Reaktionsgleichungen und eine Anwendung der Poisson Statistik:

Motivation: Ausgangspunkt der Aufgabe ist der Nachweis, dass die ADP-Entbindung des MyosinV-Motors dessen Zykluszeit bestimmt (s. Abb. 19.4) und mit dem gezeigt wurde, dass Myosin V ein prozessiver Motor ist. Dies wurde durch witzvolle Messungen der Verweilzeiten des Motors im gebundenen Zustand (Rigorzustand (MyoV-ADP) als Funktion der ADP-Konzentration gezeigt. Es ist ein sehr lehrreiches Beispiel, wie man die Kinetik gekoppelter chemischer Reaktionen aufklären kann.

Wir betrachten die Reaktionen My+ATP $LaTeX: \longleftrightarrow$ My-ATP; My-ATP $LaTeX: \longleftrightarrow$ My-ADP +P (Hydrolyse des ATP durch Myosin) und My-ADP $LaTeX: \longleftrightarrow$ My + ADP. My-ATP ist Lieferant von My-ADP. Man betrachtet zwei Szenarien. In Abwesenheit von ADP zerfällt MyADP ohne Rückbindung und ATP kann unbehindert binden. Ist ADP vorhanden, so konkurriert es mit der Bindung von ATP, d.h. ATP kann nur binden, wenn ADP dissoziiert. Der Zyklus wird verlangsamt.

Wir betrachten zuerst die Situation in Abwesenheit von ADP. Die Kinetik ist bestimmt durch den Zerfall von My-ADP und dessen Bildung durch Bindung von ATP. Zur Vereinfachung der Schreibweise benutzen wir folgende Abkürzungen ein: My-ATP=A; My-ADP = B, My = C; ATP = D und ADP = E.

Lösung der Ratengleichungen:

Die Konzentrationen seien A, B, C. Die Ratengleichungen sind nun:

Bildung (aus My-ATP) und Zerfall von My-ADP: $LaTeX: \frac{dB}{dt}=k_1A-k_2B$ Hydrolyse von My-ATP: $LaTeX: \frac{dA}{dt}=-k_3 A$

Lösung der homogenen Gleichungen: $LaTeX: B=C(t)e^{-k_2t}$ $LaTeX: A=A_0 e^{-k_1t}$

Lösung der inhomogenen Gleichung für B durch Variation der Konstanten C(t)liefert:

$LaTeX: C(t)=\frac{A_0k_1}{k_1-k_2}(e^{-(k_1-k_2)t_1})$ und damit: $LaTeX: B(t)= \frac{B_0k_1}{k_1-k_2}(e^{-k_1t-e^{-k_2t}})$ (1)

Die Wahrscheinlichkeit, dass das ADP in der Zeit t entbindet (d. h. die Verweilzeit der My-ADP-Bindung) ist dann $LaTeX: k_2B(t)$ , denn ist $LaTeX: k_2$ groß, so ist die Lebensdauer des gebundenen Zustands klein.

Lösung mit dem Konvolutionstheorem: Bei diesem Lösungsweg gehen wir von der Poisson-Gleichung aus. Diese kann zwei Fragen beantworten. Wir können erstens (wie in Aufgabe 14.5) nach der Wahrscheinlichkeit fragen, wie oft ADP in der Zeit t von Myosin entbindet. Diese ist gegeben durch $LaTeX: P(k,\mu)=\frac{\mu^k}{k!}e^{-\mu}$

Für unsere Zwecke ist eine andere Darstellung notwendig. Anstatt die Zahl der Ereignisse in einer Zeit t zu zählen, fragen wir nach dem Zeitintervall zwischen zwei Ereignissen. Diese ist gegeben durch: $LaTeX: P(t,\lambda)=\kappa e^{-kt}$ , wobei $LaTeX: \kappa$ die Wahrscheinlichkeit pro Zeit ist, dass das Ereignis eintritt. Dies wird verständlich, wenn man die mittlere Wartezeit berechnet: $LaTeX: T=\int dt t e^{-\kappa t}=\kappa^{-1}$ .

Hat man es mit zwei Wahrscheinlichkeiten zu tun, d.h. in unserem Fall mit der, dass ADP entbindet ( $LaTeX: W_1=k_1e^{-k_1t}$ ) und der, dass ATP bindet ( $LaTeX: W_2=k_2e^{-k_2t}$ ), so ist die gesamte Wahrscheinlichkeit, dass ADP entbindet durch die Konvolution von $LaTeX: W_1(t)$ und $LaTeX: W_2(t)$ gegeben. Die Konvolution der Verteilungen der Übergangswahrscheinlichkeiten ist: $LaTeX: K(k_1,k_2)=\int dt'e^{-k_1(t-t')}e^{k_2t'}$

Integriert man diese Gleichung von t=0 nach t so folgt die obige Gleichung (1). In den Experimenten von Rief et al. wurde Gl(1) an die gemessenen Verteilungen der Verweilzeiten angepasst, um $LaTeX: k_1$ und $LaTeX: k_2$ zu messen.

Zusatzbemerkung: Als weiterer Beweis dafür, dass ADP-Entbindung von MyosinV der geschwindigkeitsbestimmende Schritt des Arbeitszyklus ist, wurde in der Arbeit von Rief et al gezeigt, dass bei Anwesenheit von >400 $LaTeX: \mu M$ ADP nur eine Ratenkonstante $LaTeX: k_0$ auftritt, d.h. dass die Verweilzeit des Motors eine rein exponentielle Funktion ist. Wir betrachten dazu das Gleichgewicht My-ADP $LaTeX: \longleftrightarrow$ My + ADP. Sie sei durch die Gleichgewichtskonstante K $LaTeX: (=\frac{Myo \cdot ADP}{My-ADP})$ bestimmt. Die Ratengleichung der Entbindung von ADP ( $LaTeX: \equiv$ E) ist dann:

$LaTeX: \frac{dB}{dt}=k_1CE-k_2B=k_1KB-k_2B$ oder $LaTeX: B(t)\propto B_0 e^{-k^*t}$ mit $LaTeX: k^*=k_1K-k_2$

Die Entbindung zeigt bei hohen ADP-Konzentrationen also einen einfachen exponentiellen Zerfall.

Aufgabe 19.5:

Beweis der Hand-über-Hand-Bewegung des Myosin V-Motors

Motivation: Die Methode der Anregung der Fluoreszenz unter dem Winkel der Totalreflexion TIRF (Abkürzung für 'Total Internal Reflection Fluorescence Microscopy') eröffnet vielseitige Möglichkeiten zur Untersuchung der Reorganisation des Aktin-Zytoskeletts während der Zelladhäsion oder Zellbewegung oder zur Aufklärung elementarer Prozesse molekularer Motoren. Als eindrucksvolles Beispiel betrachten wir die Anwendung von TIRF zur hochauflösenden Aufklärung des Bewegungsmechanismus molekularer Motoren (Myosin V).

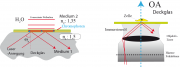
TIRF-Methode: Abb 19A.5 zeigt das Prinzip von TIRF. Das Objektiv des Mikroskops wird so konstruiert, dass die Lichtstrahlen an der oberen Oberfläche des Deckglases unter dem Winkel der Totalreflexion eintreffen. Der kritische Winkel $LaTeX: \theta_c$ der Totalreflexion ist durch die Bedingung $LaTeX: \theta_c=\frac{n_2}{n_1}$ bestimmt (s. Abb. 19A.5 rechts). Durch Verwendung von Immersionsöl wird die Einkopplung des Lichts in den Objektträger vereinfacht und gleichzeitig eine hohe numerische Apertur erreicht.

Abb. 19A.5: Links: Prinzip der TIRF Methode. Rechts: Schema eines Objektivs mit hoher numerischer Apparatur.

Für die Anwendung sind zwei Parameter entscheidend. Die laterale Auflösung und die Eindringtiefe der evaneszenten Welle in das optisch dünnere Medium ( $LaTeX: H_2O$ ). Diese Oberflächenwelle sorgt dafür, dass die Randbedingung des elektrischen Feldes an der Grenzfläche erfüllt werden und klingt exponentiell ab.

$LaTeX: E(z)=E_0e^{-\frac{z}{\eta}}$

Die Eindringtiefe am Grenzwinkel der Totalreflexion ist: $LaTeX: \eta=\frac{\lambda}{2\pi}\frac{1}{\sqrt{n_1^2sin^2(\theta)-n_2^2}}$

Eine umfassende Darstellung der Rolle der evaneszenten Welle bei TIRF: M. Kramer (Fa Zeiss) Photonic 2: p42 (2004)

Nano-Fluoreszenzmikroskopie: In Kapitel 37.3.5 hatten wir die Grundlagen der Methode eingeführt und dargestellt, wie man (unter Verwendung von CCD-Kameras) die Position von (auf einer Ebene fixierten) Fluoreszenzsonden mit nm-Genauigkeit bestimmen kann, indem man über einige tausend Fluoreszenzsignale (typischerweise $LaTeX: 10^4$ ) der Sonde aufsummiert. Wie bei spektroskopischen Methoden (z.B. NMR) muss man die Verbesserung des Signal-Rausch-Verhältnisses der Positionsbestimmung durch Zeitmittelung über einige tausend Signale bezahlen. In den Experimenten von Yildiz et al. [Yildiz et al 2003)] wurden durch Mittelung über 0.5 sec (Registrierung von ca 15000 Signalen) die Position auf 1.5 nm genau bestimmt.

Eine gute Darstellung moderner Tricks zur Verbesserung der Zahl registrierbarer Signale der Fluoreszenz-Sonde findet man in [ToDo].

Das Experiment von Yildiz et al.:

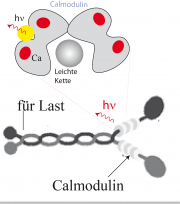
Die Motoren wurden an zwei Stellen mit Farbstoff markiert; (i) Rhodamin wurde an die leichte Kette des Motorkopfs angekoppelt; (ii) ein Cyanofabstoff (Cy3) wurde an eines der 6 Calmoduline angedockt, die an die Beine der Motoren binden und für dessen Funktion notwendig sind (s. Kapitel19.2). Da man nicht a priori sagen kann, wo die Chromophore sitzen, ist eine statistische Analyse der saltatorischen Bewegung der Farbstoffe notwendig.

Abb.19A.5b Darstellung der Markierung einer der 'leichten Ketten' von MyoV mit einem Cyano-Farbstoff. Bei den leichten Ketten handelt es sich um Proteine mit ähnlicher Struktur wie das Ca-bindende Calmodulin ( s.Kapitel 18). Unten: Links im Bild werden die nach dem Hand-über-Hand Modell erwarteten Positionen dargestellt, wenn der Motor um 2x37 nm läuft. Man beachte, dass die Fluoreszenzsonde sich beim ersten Teilschritt um $LaTeX: \Delta l=(37nm-2x)$ und beim zweiten um $LaTeX: \Delta l=(2 \cdot 37nm+2x)$ bewegt.

Abb.19A.5b Das Bild zeigt die schrittweise Bewegung eines Motors. Die Einsätze zeigen Verteilungen der Schrittweite. Der untere zeigt die Verteilung der im Bild dargestellten Trajektorien eines der analysierten Motoren, in dem nur 72 nm Schritte beobachtet werden. Das obere Histogram zeigt das Ergebnis für eine Sonde die Schritte von $LaTeX: \approx$ 23 nm und $LaTeX: \approx$ 50 nm macht. Dies entspricht einer Position $LaTeX: x\approx 7$ nm von der Längsachse des Motors.

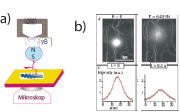
Das obere Bild in Abb.19A.5b zeigt eine Trajektorie eines mit Rhodamin markierten Motors. Alle Sprünge haben eine Länge von 72 nm, wie man nach dem Hand-über-Hand-(HÜH-) Modell erwartet. Die Verteilung der Schrittweiten gehorcht einer Gaußfunktion und hat ein Maximum bei ca. 72 nm. Die Trajektorien von an Calmodulin markierten Motoren (die wir hier nicht zeigen) zeigen Sprünge von $LaTeX: \Delta L$ =72nm, von $LaTeX: \Delta L$ =(37-15)nm und von $LaTeX: \Delta L$ =(37+15) nm, wie man nach dem HÜH-Modell erwarten würde, wenn der Abstand des Farbstoffs von Längsachse des Stamms x $LaTeX: \approx$ 7.5 nm ist. Damit wurde von Yildiz et al. ein sehr schöner und schlüssiger Beweis des HÜH-Modells erbracht.

Das schöne Experiment zeigt eindrucksvoll, wie wichtig statistische Analysen in der Biophysik sind. Man sollte aber auch beachten, dass die hohe Genauigkeit der Ortsbestimmung durch Fixierung des Aktins auf einer Ebene beruht.

Für Fortgeschrittene: Nach dem HÜH-Modell sollte die Häufigkeit der Sprünge (Sprungrate R(T)) um einen Faktor zwei kleiner sein, als die der 23 nm und 52 nm Sprünge, da der rechte Motorkopf nach Abb. 19A.5b beim Übergang A $LaTeX: \longrightarrow$ B einmal aussetzt. Man kann dieses Verhalten indirekt beobachten, wenn man die Verteilung der Schrittweiten wie in Aufgabe 19.4 analysiert. Man betrachte dazu die Schritte A $LaTeX: \longrightarrow$ B und B $LaTeX: \longrightarrow$ A'. Dann ist die Wahrscheinlichkeit der Verweilzeiten T im Zustand A durch die Funktion $LaTeX: f(t)=k_1e^{-k_1t}$ und die in B durch $LaTeX: f(t')=k_2 e^{k_2 t'}$ bestimmt. Nun haben wir in der vorherigen Aufgabe gelernt, dass unter diesen Umständen die gesamte Verteilung der Schrittweiten durch Konvolution der beiden Funktionen bestimmt ist. Wir können das Ergebnis aus Aufgabe 19.4 übertragen. Nun sind aber die Übergangswahrscheinlichkeiten gleich $LaTeX: k_1 =k_2 = k$ . In diesem Fall ist die Verteilung der Schrittweiten gegeben durch $LaTeX: P(t)=tk^2 e^{-kt}$ . Man erhält die Verteilung der Schrittweiten, indem man die Regel von Bernouilli-L'Hospital anwendet. Auch diese Vorhersage wurde in dem Experiment eindeutig bestätigt.