Lösungen Kapitel 31

From BioPhy.de Wiki

Aufgabe 31.1:

$LaTeX: \pi$ -Elektronenverteilung im $LaTeX: H_3C-C=C-CH_3$ .

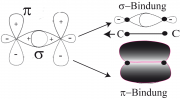
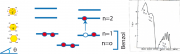
Wir betrachten in Abb. 1a zunächst die $LaTeX: \pi$ -Elektronenverteilung in der $LaTeX: \sigma$ - und $LaTeX: \pi$ -Bindung. Die Radiale Elektronenverteilungsfunktion ist: $LaTeX: \Psi = \sqrt{\frac{1}{\pi a_0^3}}^{-1}exp(-\frac{r}{a_0})$ . Dabei ist $LaTeX: a_0$ ein effektiver Atomradius, der von der effektiven Kernladungszahl abhängt, Abb. 1b zeigt die radiale Verteilung der Elektronen in dem bindenden und dem anti-bindenden (oder ersten angeregten) Zustand nach dem 'Molecular Orbital' (MO-)-Modell.

Abb. 1.a) Schematische Darstellung der $LaTeX: \sigma$ - und $LaTeX: \pi$ -Orbitale und der Bildung von $LaTeX: \sigma$ - und $LaTeX: \pi$ -Bindungen.

Abb. 2. a) Qualitative Darstellung der Elektronenverteilung in der -C=C- Bindung für die $LaTeX: \sigma$ - und $LaTeX: \pi$ -Bindung.

Eigenfunktion im Freien Elektronengas Modells:

Die Eigenfunktionen des primitiven Modells des kleinsten Polyens hat die Form:

$LaTeX: \Psi (r)= \sqrt{\frac{2}{3d}}sin(\frac{\pi x}{3d})$

(ohne alternierenden Bindungslängen), siehe Gl 31.5 . Einfache Beispiele für Moleküle mit 2 Elektronen sind Äthylen (oder Ethen) Abb.1a unten) Propylen (oder Propen), wenn ein H-Atom durch eine $LaTeX: CH_3$ -Gruppe ersetzt und das in Abb. 1a unten gezeigte trans-2-Buten. Man nennt diese Klasse von Molekülen auch Diene.

Aufgabe 31.2:

Beweis der Gl 31.5 (Anwendung des Bloch Modells des Elektronengases).

Vernachlässigt man die Alternierung der Bindungslängen der Einfach- und Doppelbindungen, so lassen sich die Energiezustände der Polyene mit dem primitiven Modell eines Teilchens in einer abgeschlossenen Kasten oder dem Bloch-Modell der freien Elektronen in einem Metallblock der Länge L berechnen. Die Schrödingergleichung hat die Form:

$LaTeX: \frac{\partial^2 \psi}{\partial x^2} + 2 \frac{m}{\hbar^2}(E-V)$

wobei E für die Energiezustände und V für die Tiefe des Potentialtopfes der Länge L steht. Für lineare Polymere hat die Wellenfunktion die Form: $LaTeX: \psi_n=A_n sin (k_nx+a_n)$ , d.h. $LaTeX: \psi$ ist periodisch: $LaTeX: \psi(r) = \psi(r+L)$ . Setzt man die Wellenfunktion in die Schrödingergleichung ein, so erhält man für die Energiezustände: $LaTeX: E_n= \frac{\hbar^2 k_n^2}{2m}$ . Zur Bestimmung der Konstanten $LaTeX: k_n$ , $LaTeX: a_n$ und $LaTeX: A_n$ benutzt man die Randbedingung, dass die Wellenfunktion an den Wänden (x=0 und x=L) verschwindet. Dies liefert sofort die Werte $LaTeX: a_n=0$ und $LaTeX: k_n= \frac{\pi n }{L}$ . Die normierten Wellenfunktionen $LaTeX: \Psi_n$ und die Energiezustände haben die Form: $LaTeX: \psi_n = \sqrt{\frac{2}{L}} sin(\frac{\pi n x}{L})$ und $LaTeX: E_n= \frac{n^2 h^2}{8mL^2}$

Bei der konkreten Anwendung auf Polyene in Kapitel 31 haben wir die Länge L des Potentialtopfs durch die Gleichung $LaTeX: L=(2n+1) d$ ersetzt, um der Alternierung der Doppel und Einfachbindungen Rechnung zu tragen.

Aufgabe 31.3:

Die Termschemata der Porphyrine mit und ohne Metallion. Zur Ursache der Soret-Bande der Metall-Porphyrine.

Zur Lösung des Problems gehen wir von den Gleichungen in Kapitel 31.2.1 aus. Die Anwendung des Blochmodells auf diese Situation lieferte die Wellenfunktion $LaTeX: \psi_l$ und die Energie $LaTeX: E_l$ :

$LaTeX: \psi_\lambda =\sqrt{\frac{1}{2 \pi}}e^{\pm i\lambda \theta}$ mit $LaTeX: E_\lambda=\frac{h^2 \lambda^2}{8m \pi^2 R^2}$ (31.7)

Da für stationäre Zustände der Elektronen die Funktionen $LaTeX: \psi (\theta)$ bezüglich $LaTeX: \theta$ periodisch sein müssen, wird $LaTeX: \lambda =\pm n$ . Die umlaufenden Elektronen haben den Bahndrehimpuls $LaTeX: B=\lambda \hbar$ . Mit Ausnahme des Zustandes $LaTeX: \lambda=0$ sind alle anderen zweifach entartet (d.h. $LaTeX: B=\pm |\lambda|\hbar$ ). Aufgrund dieser Entartung ist die Klasse der Ringsysteme mit $LaTeX: n=4r +2$ dadurch ausgezeichnet, dass alle bindenden Orbitale (mit $LaTeX: \lambda =0, \pm 1, \pm 2$ genau mit zwei Elektronen besetzt sind. Die Moleküle besitzen abgeschlossene Elektronenschalen. Für alle anderen Moleküle sind auch nicht-bindende Zustände besetzt. Abb. 1a zeigt, dass Porphyrine mit H-Atomen im Zentrum 22 während die Moleküle mit Metallionen 18 $LaTeX: \pi$ -Elektronen besitzen. Ersteres gehört zur Gruppe mit r=5 und letzter mit r=4. Beide haben also abgeschlossene Schalen, Letzteres hat eine höhere Symmetrie. Ein wichtiger Unterschied besteht jedoch darin, dass die p-Elektronen des Metallions mit den $LaTeX: \pi$ -Elektronen des Rings wechselwirken können.

Abb. 1:a. Die Struktur der Porphyrine mit H-Atomen (links) und Metallionen (rechts) im Zentrum. Die Nummern 1,2 usw. kennzeichnen die C-Atome mit $LaTeX: \pi$ Elektronen. b) Darstellung der Elektronenzustände und zweier möglicher angeregter Zustände. Rechts sind zwei Anregungszustände niedrigster Energie $LaTeX: r^3(r+1)$ und $LaTeX: -r^3-(r+1)$ dargestellt bei denen die Drehimplusänderung $LaTeX: \Delta \lambda =1$ ist. Alle Übergänge mit $LaTeX: \Delta \lambda =0, \pm 1, \pm 2$ sind möglich. Höhere Anregungszustände sind beispielsweise $LaTeX: r^3(r+2)$ mit $LaTeX: \Delta \lambda=2$ .

Abb.2. (a) Vergleich der Absorptionsspektren des Porphyrins ohne (oben) und mit einem Zn-Metallion (unten). Beide Spezies besitzen zwei Absorptionsbanden, eine starke Soret-Bande im UV( $LaTeX: \approx 400nm$ ) und eine schwächere Bande im Sichtbaren. In Gegenwart des Metallions verschmelzen die vier getrennten Banden im Sichtbaren. Dadurch wird die Farbe der Moleküle bestimmt. (b) Die gestrichelten und durchgezogenen Kurven markieren die Wellenfunktionen (bzw. Elektronenverteilungen) nach der MO-Theorie und definieren die Knoten des obersten besetzten und des untersten unbesetzten Zustandes. Nach M. Gouterman (1961) J. of Molecular Spectrocopy 6: 138-163)

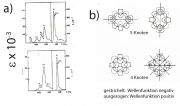
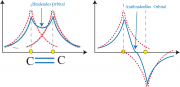
Zur Zahl der Knoten und den Absorptionsspektren:

Man sieht anhand von Abb. 1b leicht ein, dass der oberste besetzte Zustand des 18-Elektronensystrems vier Knoten und der niedrigste Anregungszustand 5 Knoten besitzt. Das Metallion wechselwirkt besonders stark mit dem Zustand mit 4 Knoten, da dann maximale Überlappung der p- und der $LaTeX: \pi$ -Elektronen stattfindet. Die vier Banden des sichtbaren Spektrums verschmelzen und die Farbe wird intensiver. Die Position der sichtbaren Absorptionsbande hängt von der Elektronenstruktur der Metalle ab. Sie liegt für Mg-Porphyrine bei etwa 650 nm und für Fe oder Co bei etwa 550 nm. Die sichtbare Bande des Hämoglobins liegt bei 550 nm (s. auch Aufgabe 31.4).

Aufgabe 31.4:

Warum ist Chlorophyll grün und Hämoglobin rot?

Die sichtbare Farbe ist primär durch die Wellenlängenabhängigkeit der Reflektivität R bestimmt. Für senkrechten Einfall ist die Reflektivität durch den komplexen Brechungsindex $LaTeX: n*=n-i\kappa$ bestimmt, wobe n der Real- und $LaTeX: \kappa$ der Imaginärteil ist. Letzterer ist ein Maß für den Absorptionskoeffizienten $LaTeX: \epsilon$ . Es gilt $LaTeX: \epsilon =\frac{4\kappa}{\lambda}$ . Die Reflektivität für senkrechten Einfall des Lichts ist eigentlich durch die Fresnel-Gleichung gegeben:

$LaTeX: R=\frac{(n-1)+\kappa^2}{(n+1)+\kappa^2}$ (1)

Für kleine Brechungsindizes des Materials hat das Reflektionsspektrum eine ähnliche Form wie das Absorptionsspektrum. Allerdings wird das Spektrum durch die Absorption des Lichts und die Streuung durch das Material verfälscht.

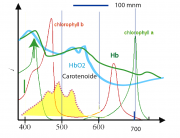
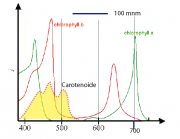
In Abb1 zeigen wir die Überlagerung der Absorptionsspektren des Chlorophylls, des Hämoglobins (mit und ohne Sauerstoff) sowie von Carotenoiden. Chlorophyll besitzt zwischen der Soret-Bande und der langwelligen Absortion einen Bereich schwacher Absorption und daher zeigt es ein Licht grüner Farbe. Die Soret-Bande des Hämoglobins reicht bis in den grünen Bereich. Daher erscheint Blut rot. Das Absorptionsvermögen des oxidierten Blutes ist im roten Bereich wesentlich keiner als das von Hb. Aus diesem Grund erscheint das $LaTeX: O_2$ -haltige Blut heller. Diese Verhalten nutzte Robert Mayer bei der Entdeckung des Energiesatzes (s. Kapitel 1)

Abb1: Vergleich der Absorptionsspektren von Chlorophyll,Chlorophyll b und Hämoglobin mit (HbO $LaTeX: _2$ ) und ohne (Hb) Sauerstoff.

Aufgabe 31.5:

Der langwelligste Übergang des Benzols im FEG-Modell.

Die Wellenfunktionen des obersten besetzten und des untersten unbesetzten Zustands haben die Form:

$LaTeX: \psi_1 =const \cdot e^{\pm i\frac{\Theta}{6}}$ mit $LaTeX: E_\lambda = \frac{\hbar^2}{2mU^2}$ ; $LaTeX: \psi_2 =const \cdot e^{\pm i\frac{\Theta}{3}}$ mit $LaTeX: E_\lambda = \frac{4 \hbar^2}{2mU^2}$

Der Energieunterschied ist $LaTeX: \Delta E=\frac{3 \hbar^2}{2mU^2}$ . U ist der Umfang des $LaTeX: \pi$ -Elektronensystems. Für Benzol ist U=6 mal $LaTeX: 0.14 nm$ = $LaTeX: 0.84 nm$ .

Abb. 1: Zum Energieschema im FEG- Modell. Nur jeweils eine Elektronenverteilung in den Zuständen $LaTeX: \lambda=1$ und $LaTeX: \lambda=2$ werden gezeigt. Die anderen erhält man durch Rotation um $LaTeX: \Theta=30$ \degree. Rechts: Absorptionsspektum des Benzols.

Mit der Elektronenmasse m= $LaTeX: 9 \cdot 10^{-31}$ kg und h = $LaTeX: 6.6 \cdot 10^{-34} J s$ erhält man für die Anregungsenergie $LaTeX: 2\cdot 10^{-19}$ J. Das entspricht $LaTeX: 250 k_BT$ oder $LaTeX: \frac{240}{40} eV = 6 eV$ oder einer Absorptionswellenlänge von 200 nm. Die langwelligste Bande des Benzols liegt bei 240 nm. In Anbetracht der groben Näherung ist die Übereinstimmung befriedigend. Allerdings berechnet man die Energiezustände der Aromaten in der Regel mit der LCAO Methode von Hückel, die in der Monogarphie von Murrell [1] gut dargestellt ist.

Aufgabe 31.6:

Zur Oszillatorenstärke

Die Aufgabe dient dazu sich mit dem etwas sperrigen Thema der Oszillatorenstärke vertraut zu machen. Erinnerung an einige Definitionen:

1. Das Übergangsmoment: $LaTeX: <\psi_k|e\vec{r}|\psi_l>=\vec{M_{kl}}=\int \psi_k(r) e\vec{r} \psi_l^*(r) dV$ .

$LaTeX: M_{kl}$ hat im SI-System die Dimension [ $LaTeX: M_{kl}$ ] = $LaTeX: 1 Debye =3.34 10^{-30} Cb m$ .

2. Der Molaren Extinktions-Koeffizienten $LaTeX: \epsilon$ ([ $LaTeX: \epsilon$ ]= $LaTeX: 1 \frac{L}{M\cdot cm})$ wird mit Hilfe des Lambert-Beerschen Gesetzes bestimmt.

$LaTeX: \frac{I}{I_0} = 10^{-\epsilon c d} = e^{- \epsilon cd ln(10)}$ (2)

3. Da $LaTeX: \epsilon$ von der Wellenlänge $LaTeX: \lambda$ abhängt, benutzt man die Oszillatorenstärke f als Maß für die Stärke eines elektronischen Übergangs der aus mehreren Schwingungsbanden besteht $LaTeX: f_{kl}=const \cdot \int \epsilon_{kl}(\lambda)d\lambda$ . Der Vorfaktor const wird so gewählt, dass f dimensionslos ist. Zwischen f und $LaTeX: M_{kl}$ besteht folgender theoretischer Zusammenhang:

$LaTeX: f_{kl}=\frac{8 \pi^2 mv}{3 he^2}|M_{kl}^2|$ (3)

Man benutzt zur Umrechnung als Einheit der Ladung [e]= $LaTeX: 1 cm$ $LaTeX: dyn^{\frac{1}{2}}$ oder 1 esu $LaTeX: \approx 3.3 \cdot 10^{-10} C$ . Im SI-System erhält man mit Gl.(3) den numerischen Zusammenhang: $LaTeX: f_{kl}=14.8\cdot 10^{41}<v_{kl}>\cdot |M_{kl}^2|$

Frage 1: $LaTeX: \lambda=500 nm$ entspricht $LaTeX: \lambda= 0.6 \cdot 10^{15}Hz$ . Die Oszillatorenstärke f =0.25 liefert ein Übergangs-Dipolmoment von $LaTeX: M_{kl}= 0.16 \cdot 10^{-28}$ Cbm oder 0.2 Debye.

Frage 2: Der Vorfaktor im esu-System wird mit Gl.(3) berechnet. Bei der Berechnung ist zu beachten, dass das Planck'sche Wirkungsquantum h und die Elektronenmasse m in cgs Einheiten und nicht in mkgs-Einheiten eingesetzt wird. Im cgs/esu-System ist $LaTeX: f_{kl}=4.7\cdot 10^{29}<v_{kl}>\cdot |M_{kl}^2|$ .

Aufgabe 31.7:

Eigenschaften des Dipolstrahlers und das Konzept der optischen Nahfeld-Mikroskopie (SNOM).

Zur Behandlung dieser Aufgabe ist es hilfreich, sich mit den Grundlagen der Strahlung eines Hertzschen Dipols (Dipolmoment $LaTeX: \mu (t)= \mu_0 sin(\omega(t-\frac{r}{c})$ ) vertraut zu machen. Eine einfache Darstellung findet man z.B. in 'Theorie der Elektrizität' von Becker und Sauer. Das zeitabhängige elektrische Potential ist durch das retardierte Potential $LaTeX: \phi$ bestimmt, das man nach Potenzen des Abstands r entwickelt. Das Potential hat im SI-System die Form:

$LaTeX: \phi=\frac{2 \pi \mu_0 \vec{r}}{\lambda 4 \pi \epsilon_0 r^2}cos(\omega(t-\frac{r}{c}))+\frac{\mu_0 \vec{r}}{4 \pi \epsilon_0 r^3}sin(\omega(t-\frac{r}{c}))\epsilon$ (1)

Aufgabe 1:

Das Fernfeld: Dieses ist durch den ersten Term in Gl(1) gegeben, der durch das retardierte elektrische Potential des Dipols bestimmt ist. Für die erste Aufgabe interessiert nur der Poyntingvektor. Dieser ist gleich der in die drei Raumrichtungen abgestrahlte Energie und hat die Dimension Energie pro Fläche und Zeit (und wird oft in $LaTeX: \frac{Watt}{s \cdot m^2}$ gemessen). Der Energiefluss eines Dipolstrahlers der in eine feste Richtung schwingt hat die Form:

$LaTeX: \vec{S}= \frac{\omega^4 \mu_{el}^2}{(4\pi)^2\epsilon_0 c^3 }\frac{\vec{r}}{r^3}=\frac{\omega^4 \mu_{el}^2}{4\pi \epsilon_0 c^3}sin^2 \theta$ $LaTeX: \frac{Watt}{m^2 s}$

Zur Berechnung der gesamten abgestrahlten Energie integriert man den Vektor S über den Raumwinkel $LaTeX: d\Omega=sin \theta d\theta d\phi$ und erhält $LaTeX: <S>=\frac{\omega^4 \mu_{el}^2}{12 \pi \epsilon_0 c^3}$ . Dies ist das berühmte Gesetz von Rayleigh, nach dem die von den Molekülen eines Gases gestreute Energie mit der 4ten Potenz der Frequenz zunimmt und beispielsweise für das Blau des Himmellichts verantwortlich ist. Man beachte noch, dass wir in dieser Aufgabe den Brechungsindex des Vakuums benutzten.

Das Nahfeld: Offenbar fällt der erste Term wesentlich langsamer mit dem Abstand r ab als der zweite und kann für kleine r (d.h. im Nahfeld) vernachlässigt werden. Das elektrische Feld hat dann dieselbe Form, wie das statischen Potential und das magnetische Feld hat dieselbe Form wie ein Stromelement der Länge $LaTeX: \Delta l$ des Dipols: $LaTeX: \frac{dp}{dt}$ . Die Felder sind (im SI System) gegeben durch:

$LaTeX: \vec{E}=-\frac{\vec{\mu}}{4 \pi \epsilon_0 r^3} + \frac{3 (\vec{p}\vec{r})\vec{p}}{4 \pi \epsilon_0 r^5}$ und $LaTeX: \vec{H}= \frac{(\vec{r} \frac{d\vec{\mu}}{dt})}{r^3}$ (2)

E hat die Dimension $LaTeX: \frac{V}{m}$ und H $LaTeX: \frac{A}{m}$ . Das Produkt S=EH ist ein Maß für den Energieinhalt und hat die Form $LaTeX: S \propto \frac{\omega p^2}{4 \pi \epsilon_0 r^5}$ (Dimension: $LaTeX: \frac{Watt}{s \cdot m^2}$ ). Die Energie des Nahfeldes breitet sich nicht aus, sondern bleibt an dem Dipol lokalisiert.

Das Dipolmoment sei 1 Debye ( $LaTeX: =3.34 \cdot 10^{-30} Cb m$ ), $LaTeX: \epsilon_0=8.8 \cdot 10^{-12} \frac{As}{Vm}$ , $LaTeX: \lambda= 500 nm$ entspricht $LaTeX: \approx 10^{15} Hz$ . Es wird $LaTeX: S \approx 10^{-34}r^{-5}$ . Erhöht man den Abstand von 1nm (was etwa der Dimension des Dipols entspricht) auf 5 nm (was etwa dem Försterradius entspricht) so wird die Energie um den Faktor 3000 abgeschwächt. Man kann sich ausrechnen, dass die Intensität des Nahfeldes in 1 nm Abstand etwa so groß ist wie die des Fernfeldes in 1 $LaTeX: \mu m$ Abstand.

Aufgabe 3: Das Nahfeldmikroskop funktioniert (grob gesagt) ähnlich, wie das Stethoskop mit dem der Arzt Herzgeräuche lokal analysiert. Man bringt den Empfänger so nah an den Sender (der ein Dipolstrahler sei), dass nur die Nahfeldkomponente des Poynting-Vektors registriert wird. Als Empfänger dient z-B. eine ausgezogenen Pipette mit eine sehr kleinen Öffnung, die meist außen verspiegelt ist und das Licht zum Detektor leitet. Das Bild entsteht durch Rastern des Objekt. Daher ist die Methode derzeit nur zur Untersuchung von Oberflächen geeignet. Die Pipette muß dabei im Abstand von 1-10 nm über das Objekt bewegt werden.

Aufgabe 31.8:

Lichteinfang durch eine Thylakoidvesikel.

Wie Abb. 30.3 am Beispiel der bakteriellen Reaktionszentrums zeigt, umgeben die Lichtsammlerkomplexe die Reaktionszentren. Die Situation bei Thylakoid-Membranen ist komplizierter und weniger bekannt. Sie enthalten drei Gruppen von Proteinkomplexen mit hohem Anteil an Chromophoren: Photosystem I, Photosystem II und Cytochromes b/f (s. Abb 31.7). Wir nehmen an, daß die Lichtsammlerkomplexe hauptsächlich das Photosystem II umgeben und etwa 300 Chlorophylle enthalten. Diese absorbieren bei 680 nm und der molare Extinktionskoeffizient sei 70.000 $LaTeX: \frac{L}{Mol\cdot cm}$ . Reaktionszentren RZ II bedecken etwa 50 \

Abb. 1. Anordnung der Photosysteme in Thylakoidmembranen.

Unter der Annahme, dass das Lambert Beersche Gesetz gilt, können wir mit den obigen Angaben die mittlere Konzentration in $LaTeX: \frac{Mol}{L}$ wie folgt abschätzen: Die mittlere Flächendichte der RZ ist $LaTeX: \rho \approx 3\cdot 10^{17}$ Chlorophylle pro $LaTeX: m^2$ . Das entspricht einer Konzentration in Lösung von $LaTeX: 3 \cdot 10^{14}$ Chlorophylle pro Liter, oder $LaTeX: c \approx 5 \cdot 10^{-10} \frac{Mol}{L}$ . Mit Gl 38.19 folgt: $LaTeX: \frac{I}{I_0} = e^{- \epsilon cd ln10} \approx exp{-0.0001}$ ; oder $LaTeX: \frac{\Delta I}{I} \approx 10^{-4}$ . Unter Einsatz von Lasern kann man relative Absorption $LaTeX: \frac{\Delta I}{I} = 10^{- 5}$ gerade noch nachzuweisen.

Referenzen: 1 Glick, RE. (1986)Freeze fracture analysis of thylakoid membrane and Photoisystem I and II Enriched fractions of Phormidium laminosum, J. Cell Sd. 80, 57-73 (1986) 57 2 Simpson, DJ.(1984) Freeze-fracture ultrastructure of thylakoid membranes in chloroplasts from manganese-deficient plants. Plant Physiol. 74: 735 - 741.

Aufgabe 31.9:

Zum photophysikalische Zusammenspiel von Chlorophyll und Carotin.

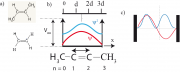
Antworten zu den Fragen:

Abb 1: Oben: Vergleich der Absorptionsspektren der Chlorophylle und des $LaTeX: \beta$ -Carotins. Abb 31.2 zeigt die Spektren bei größerer Empfindlichkeit, so dass man die Schwingungsbanden erkennt. Unten: Vergleich des Absorptions- und Fluoreszenzspektrums von $LaTeX: \beta$ -Carotin (nach Gillbro und Gogdell (1989) Carotin fluorescence Chem. Phys. Letters 158: 312-316). Vergleich der Energiezustände von Carotin und Chlorophyllen und des Energietransfers (nach [1] . Ein direkter Nachweis des Energietransfers vom Zustand S2 (1Bu+) des $LaTeX: \beta$ -Carotins zu Chlorophyll in Photosystem I von Cyanobakterien wurde durch Messung der Lebensdauer das Carotins mit Femtosekunden-Spektroskopie beobachtet. Die Lebensdauer wird durch den Transfer von 150 auf 60 fs, reduziert. [2]

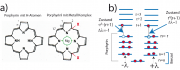
1. Die linke Abbildung zeigt, dass sich die Absorption der Carotine vom Bereich der Soretbande der Chlorophylle bis in das Sichtbare erstreckt. Der langwelligste Übergang ist verboten, wie das mittlere Bild rechts zeigt. Durch die Anordnung der elektronischen Übergänge hilft Carotin beim Einsammeln von Licht und kann die Energie direkt an die Chlorophylle weiter geben. 2. Die Spektren der Carotine und der Chlorophylle zeigen eine ausgeprägte Schwingungsstruktur, wie vor allem Abb. 31.2 zeigt. Zum Vergleich der Energien beachten wir die Umrechnungsfaktoren zwischen der Wellenzahl $LaTeX: \hat{\nu}=\frac{1}{\lambda}$ (die in $LaTeX: cm^{-1}$ angegeben wird) und der Wellenlänge, die in $LaTeX: \mu m$ angegeben wird:

$LaTeX: \lambda (nm) = \frac{10^7}{\hat{\nu}}$ ; $LaTeX: \nu (Hz)=3 \cdot 10^{10} \hat{\nu}$ ; $LaTeX: h\nu (eV)= \frac{1}{8065} \hat{\nu}$ .

Die Energien der elektronischen Übergänge liegen bei 2 eV ( $LaTeX: \approx 600nm$ ), 2.5 eV (500 nm) und 3.3 eV (450 nm). Die Energiedifferenzen der Übergänge zwischen den Schwingungszuständen liegen bei $LaTeX: \Delta \nu \approx 25 nm$ oder $LaTeX: \frac{1}{4} eV$ .

3. Da die Emissions- und Absorptionsspektren des Carotins symmetrisch angeordnet sind verschiebt sich die Gleichgewichtslage nicht (s. Abb1. Mitte).

Referenzen:

1 Schieferman-Harms D. (1985) Carotenoids in photosynthesis. I. Location in photosynthetic membranes and light-harvesting function. Biochim. Biophys. Acta 811: 327- 355.

2 Weerd et al. (2003) ß-Carotene to chlorophyll singlet energy transfer in the photosystem I core of Synechococcus elongatus proceeds via the ß-carotene S2 and S1 states. J. of Phys. Chem. 107: 5995-6002.

Aufgabe 31.10:

Hybridisierung der C-Atome für Acethylen.

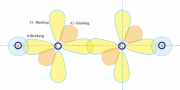
Die Aufgabe lässt sich mit dem in Kapitel 31.A beschriebenen Grundlagen leicht lösen. Im Falle der Dreifachverbindung steht nur ein $LaTeX: \sigma$ -Elektron für die C-C-Bindung zur Verfügung, während die 2p-Elektronen zwei senkrecht aufeinander stehende $LaTeX: \pi$ - $LaTeX: \pi$ -Bindungen bilden können. Die Wellenfunktionen der $LaTeX: \sigma$ -Elektronen haben die Form:

$LaTeX: \sigma_{1,2}= \frac{1}{\sqrt{2}}(\psi(2s) \pm \psi (2p_{x,y}))$

Abb.1 Die Elektronenverteilung der sp-Hybride und der p-Elektronen der C-C-Dreifachbindung.

Es soll aber nochmals erwähnt werden, dass das Konzept der Hybridisierung nur ein Hilfsmittel ist, um Eigenschaften der Moleküle mit Hilfe der einfachen quantenchemischen Modelle, (d.h. der MO-Theorie und dem LCAO-Modell) zu berechnen. In modernen quantenchemischen Methoden wendet man auch häufig die LCAO-Näherung an. Man berechnet die Wellenfunktionen nach der Hartree-Fock Methode, indem man die Wechselwirkung eines Elektrons mit der mittleren Elektronenverteilung der anderen Elektronen betrachtet. Die Orbitale werden so variiert, dass der Erwartungswert der Energie des Elektronenzustandes einen Minimalwert annimmt. Man benutzt dabei nicht mehr die klassischen Atom-Wellenfunktionen (wie in Aufgabe 31.1) sondern beschreibt die Verteilung Elektronendichte mit Gaußfunktionen. Die Übereinstimmung der berechneten Energiezustände mit den experimentellen Daten wird dabei verbessert. Die in Kapitel 31 beschrieben einfachen Konzepte bleiben jedoch erhalten.

Search

Navigation

SEARCH

TOOLBOX

LANGUAGES