03.26Strukturuntersuchung mit Kleinwinkelstreuung
Appendix 37.A: Strukturuntersuchung mit Kleinwinkelstreuung
- Vorbemerkung:
- Kleinwinkelstreuung sphärischer Partikel: Das Guinier Gesetz
- Die Guinier-Näherung
- Das Guinier-Gesetz
- Das Porod Gesetz
- Der Atomformfaktor
- Eine Anwendung: Messung der Massenverteilung in Partikel mit sphärischer Symmetrie.
- Kleinwinkelstreuuung stäbchenförmiger Moleküle
- Kleinwinkelstreeuung dünner Plättchen und dünner Schalen
- Anwendung der Neutronenkleinwinkelstreuung
- Bestimmung der Membranstruktur und der Lipid Phasendiagramme
- Feinstruktur der Aktinbündel
- Referenzen:
Vorbemerkung:
Die Bestimmung der Struktur komplexer Materialien oder supramolekularer Komplexen mit Streumethoden ist eine mühsame aber unausweichliche Aufgabe der Materialforschung und der Biophysik. Die Aufgabe wird nur dadurch etwas vereinfacht, dass die physikalischen Grundlagen der Streuung von Neutronen (engl. small angle neutron scattering (SANS)), Licht (small angle X-ray scattering, SAXS)) oder Elektronen denselben Gesetzen genügen.
Der entscheidende Punkt ist, dass die Streuung der Wellen durch das Material alleine durch lokale Fluktuationen der Dichte bestimmt ist. Dies wurde erstmals von Smoluchowski (1908), Einstein (1910) und Zernicke (1915) erkannt und theoretisch begründet. Diese internen Schwankungen in der Materie lassen sich jedoch über die Theorie der Schwankungen mit phänomenologischen Parametern korrelieren, So erhält man beispielsweise die Kompressibilität aus den Schwankungen der Dichte oder die chemischen Potentiale der Moleküle () in einer Lösung aus den Konzentrationsfluktuationen. Eine knappe aber gut verständliche Darstellung der Lichtstreuung findet man in dem Übersichtsartikel von Brunner und Dransfeld in dem Buch Biophysik von W. Hoppe et al (Springer Verlag 1983). Wir werden diese Methode daher nicht weiter behandeln. Wir konzentrieren uns hier auf die Darstellung der Grundlagen der Kleinwinkelstreuung mit Röntgenlicht und Neutronen. Diese ist als Hilfe bei der Lösung der Übungsaufgaben gedacht.
Zur Darstellung der Theorie der Kleinwinkelstreuung definieren wir in Abb. 37.A.1 zuerst die Streugeometrie. und
sind die Wellenvektoren der einfallenden und der gestreuten Welle. Die Amplitude zweier interferierender Wellen, die von verschiedenen Stellen des Materials ausgehen, ist durch deren Phasendifferenz
bestimmt. Diese ist durch die Differenz der Strecken OP-OM bestimmt und ist daher:
wobei der Radiusvektor zwischen den beiden betrachteten Punkten ist. Diese Gleichung gilt ganz allgemein und man nennt den Vektor
den Streuvektor.
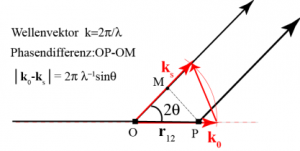
Abb. 1: Zur Definition der Streugeometrie. Die Beträge der Wellenvektoren
Kleinwinkelstreuung sphärischer Partikel: Das Guinier Gesetz
Wir betrachten zunächst die Streuung einer Suspension von Kugeln homogener Elektronendichte . Die Streuamplitude besteht aus dem scharfen Reflex Beitrag des Primärstrahls und dem gebeugten Wellen. Wenn die kolloidalen Partikel voneinander unabhängig sind, hat die Amplitudenverteilung der gestreuten Welle die folgende Form:
mit
Man nennt auch den Strukturfaktor. Gleichung 37A.2 folgt aus dem ersten Schritt der Abbe’schen Theorie der Abbildung. Die Streuamplitude in der Zwischenbildebene ist proportional zur Fouriertransformierten der Dichteverteilung des Materials. Wenn die Partikel in einem Medium der Dichte
eingebettet sind, ist die Amplitude proportional zur Differenz der Dichten der Partikel und des Mediums:
-
. In der Neutronenbeugung bezeichnet man
auch als Streulängendichte (engl. scattering length density).
Wir betrachten zunächst den Grenzfall sehr kleiner Streuwinkel . Für diesen wird
und es folgt für die Streuamplitude:
wobei V das Volumen der Kugel ist. In der Regel betrachtet man die normierte Streuamplitude:
Wie in §10 ausführlich begründet wurde, bestimmt man im Experiment den differentiellen Streuquerschnitt. Dieser hat die Form:
Diese Gleichung ist das zentrale Ergebnis der Streutheorie.
Die Guinier-Näherung
Die zentrale Aufgabe der Kleinwinkelstreuung ist die Bestimmung der Dichtverteilung der Partikel mit inhomogener Verteilung der Atome durch inverse Fouriertransfomation der Gleichung 37A.4. Wie im Fall der Röntgenbeugung an Kristallen ist dies nicht generell möglich, da die Vorzeichen der Amplituden die zu einer beobachteten Intensitätsverteilung beitragen nicht bekannt sind. Noch problematischer ist, dass man nur die Projektionen der Dichteverteilung der Partikel in Richtung des einfallenden Strahls messen kann. Falls die Teilchen kugelsymmetrisch sind kann man das Problem lösen, da man die Vorzeichen der Amplitudenverteilung kennt, wie wir im Folgenden sehen werden.
Befinden sich in der Lösung N Kugeln, so ist die gesamte Streuamplitude der Lösung . Wenn die Dichte homogen ist, kann das Integral leicht umschreiben, indem man Skalarprodukt
durch
ersetzt und über den Winkel von
bis
integriert, wobei man beachten muss, dass das Volumenelement
ist. Man erhält dann:
Die gestreute Intensität ist daher von der Form:
Für homogene Kugeln kann man das Integral relativ leicht lösen und es lässt sich mit einiger Mühe zeigen dass die Streuamplitude die folgende Form hat (s. Aufgabe 37.3 und 37.4):
Wir betrachten nun zwei wichtige Grenzfälle: und
:
Das Guinier-Gesetz
Es folgt aus der Betrachtung des Grenzfalls sehr kleiner Streuwinkel . Wenn man die rechte Seite von Gl. 37A.8 bis zu Glied fünfter Ordnung entwickelt, erhält man für die gestreute Intensität:
Dies ist aber die erste Näherung einer Exponentialfunktion der Form
Diese Gleichung hat eine anschauliche und überraschen einfache Bedeutung, wie folgende Betrachtung zeigt: Die Struktur und Größe eines Teilchens wird in der klassischen Physik durch seinen Gyrationsradius bestimmt. Dieser ist wie folgt definiert:
wobei die Verteilung der Dichte innerhalb des Teilchens ist. Für kugelförmige Teilchen homogener Dichte folgt:
Für eine Kugel hat diese den Wert und das Guinier Gesetz wird
Aus dieser Gleichung folgt eine sehr einfach Regel zur Messung der Gyrationsradien der Teilchen. Man trägt als Funktion des Wellenvektors
auf und erhält den Gyrationsradius aus der Steigung der Kurve im Bereich
Das Porod Gesetz
Im Grenzfall sehr großer Streuvektoren erhält man:
Die Streuintensität fällt also sehr schnell, d.h. mit der vierten Potenz des Streuvektors ab.
Das Guinier Gesetz des Grenzfall gilt für jede Form der streuenden Partikel. Andererseits hängen die Streukurven mit zunehmendem Streuwinkel immer stärker von der Form ab. Dies eröffnet die Möglichkeitm auch etwas über die Form der Partikel zu lernen. Dabei geht man wie folgt vor: Man startet von einer wahrscheinlichen Form und berechnet die Streukurven. Dann verfeinert man das Modell so lange, bis die berechnete Streukurve mit der gemessenen übereinstimmt.
Der Atomformfaktor
Setzt man in die Gl. 37A.6 die Elektronendichte ein, so ist das Integral Atomformfaktor. Er bestimmt den Beitrag der Atome zur Intensität der gebeugten Wellen. In diesem Fall ist der Normierungsfaktor des Nenners gleich der Zahl der Elektronen des Kerns.
Eine Anwendung: Messung der Massenverteilung in Partikel mit sphärischer Symmetrie.
Das Wunschziel der Streuexperimente ist die Messung der Dichteverteilung in den Partikeln. Dies geht nur dann wenn diese nur vom Radius r abhängt. In diesem Fall kann man
durch inverse Fouriertransformation von Gl. 37A.6 gewinnen:
wobei wieder ist.
Bei der Bestimmung von macht man von der Kenntnis Gebrauch, dass die Amplitude bei Erhöhung von q bei jeder Nullstelle das Vorzeichen wechselt. Es entsteht daher eine Folge von Maxima der Streuintensität, deren Abstand im Fall der Kugel durch den Kugelradius bestimmt ist. Besitzt der streuende Körper eine innere Struktur, so wird die Verteilung der Maxima auf charakteristische Weise modifiziert. Der Experte bekommt daher schnell eine Vorstellung von der Form und der innere Struktur der Objekte. Abb. aus dem Artikel von Svergun und Koch [1] zeigt einige charakteristische Streukurven. Sie zeigen wie sich die Streukurven verändern, wenn man die Gestalt der Kugel ändert.
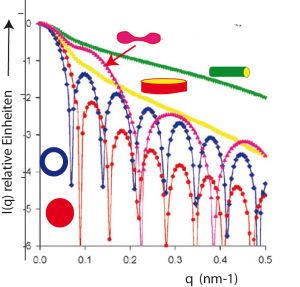
Abb 2: Charakteristische Streukurven
Eine sehr elegante Anwendung der Kleinwinlelstreuung zeigt die Messung der Dichteverteilung in Lipoprotein-Partikel in Abb. (modifiziert nach Laggner, P. et al [2]).
Die Lipoproteine (Low density lipoproteins und high density lipoproteins) sind quasisphärische Partikel, die eine zentrale Rolle für den Transport von Lipiden, Fetten und Cholesterol in Zellen dienen. Sie bestehen aus einer Kapsel aus Lipid-Protein Membranen, die mit den hydrophoben Fetten (Triglyzeride) und Cholesterol-Estern gefüllt sind. Sie werden von spezifischen Zellrezeptoren erkannt und ihre Endozytose erfolgt über ummantelte Einstülpungen und Vesikel (coated pits).
Abb. zeigt die Messung der Streukurven und die daraus bestimmte Massendichte. Man erkennt sehr deutlich den zwiebelartigen Aufbau der Komplexe. Bei der Körpertemperatur 37 \degree C wird die schichtartige Anordnung der Fette und Cholesterolester aufgebrochen, wie die abrupte Änderung der Dichteverteilung oberhalb 21\degree zeigt.
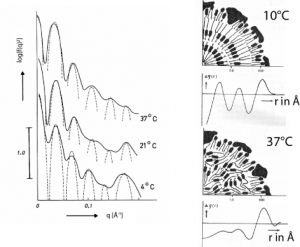
Abb 37.A3:a) Mittels Röntgen-Kleinwinkel-Streuung (XANS) bestimmte Streukurven humaner Lipoproteine für verschiedene Temperaturen. Die gestrichelten Bögen zeigen die Maxima und Minima der Amplitudenverteilung. b)Aus den Streukurven bestimmte Verteilung der Elektronendichte (untere Bilder) und den daraus abgeleiteten Modellen der Lipoproteine unterhalb und oberhalb der Umwandlung des Kerns.
Kleinwinkelstreuuung stäbchenförmiger Moleküle
Viele biologische Makromoleküle wie Aktin und Mikrotubuli sind stäbchenförmig. In einer sehr umfangreichen Arbeit hat Porod die Streuamplituden für solche Partikel berechnet [3]. Für unendlich lange Stäbchen mit dem Radius R (ohne periodische Strukturen in Richtung der langen Achse) berechnete er mit Hilfe von Gl. 37A.6 folgende Gleichung für die Streuintensität abgeleitet:
ist die Differenz zwischen den Elektronendichten des Objekts und der Umgebung im Fall der SAXS und der Differenz der Streulängendichten im Fall von SANS. Der Gyrationsradius ist in diesem Fall durch die Länge L des Stäbchens bestimmt:
Der wesentliche Unterschied zur Guinier-Gleichung für Kugeln besteht darin, dass aus zwei Faktoren besteht: Der Gaußfunktion und dem sogenannten Lorentzfaktor
Kleinwinkelstreeuung dünner Plättchen und dünner Schalen
Für den Fall sehr dünner Plättchen (der Dicke d) wurde von Porod die folgende Amplitudenverteilung abgeleitet:
Um den Unterschied zur Kleinwinkelstreuung kugelförmiger Teilchen herauszustellen, kann man die rechte Seite der Gleichung wieder nach qd entwickeln und erhält nach einiger Umrechnung die Gleichung
Der Gyrationsradius eines Plättchens der Dicke d ist und man erhält wieder ein Guiniergleichung für Plättchen und Schalen der Form :
Der wesentliche Unterschied zum Streugesetz der Kugel ist wieder der Lorentzfaktor der nun die Form hat. Zur Messung des Gyrationsradius trägt man nun das Produkt
als Funktion von q auf.
Anwendung der Neutronenkleinwinkelstreuung
Im Fall der Röntgenbeugung muss man die Elektronenverteilung kennen, um die Streufunktionen zu berechnen und mit Modellen zu vergleichen. Zur Neutronenbeugung tragen vorwiegend die Protonen bei, weshalb die Methode für Untersuchungen biologischer Materialien besonders attraktiv ist. Ein Nachteil der Neutronenbeugung ist jedoch die geringere Auflösung. Dieser Nachteil wird durch die Möglichkeit der Kontrastvariation kompensiert. Da die Neutronen nur durch die Fermi-Kontaktwechselwirkung mit den Kernen wechselwirken, kann die Dichte als Summe über -Funktionen darstellen
Dabei ist bi die Streulängendichten der Kerne. Der Vorteil der Neutronenbeugung liegt an den stark unterschiedlichen b-Werten für Protonen und Deuteronen und dem negativen Wert für Protonen:( cm ,
). Da die anderen Hauptbestandteile biologischer Materialien (O, C, N und P) Werte zwischen 0.5 und
cm haben, kann man durch Mischen von H
O und D
O die mittlere Streulängendichte des Lösungsmittels an den Wert der Proteine, DNA und Lipide anpassen und so einzelne Komponenten der Materialien beim Streuexperiment ausblenden. Die mittlere Streulängendichten der Lipidmoleküle werden bei ca 10%
-Anteil gleich dem des Wassers. Bei Proteinen und DNA erfolgt die Kontrastanpassung (engl. contrast matching) bei einem
-Gehalt von 40% und 70%. Kennt man die ungefähre Struktur der betrachteten Moleküle, so kann man deren Streulängen abschätzen und die Streukurven berechnen. Durch Vergleich berechneter und gemessener Streukurven lässt sich das Modell schließlich sukzessive verbessern. In den Zentren für Neutronenbeugung gibt es für die Auswertung der Streuexperimente ausgefeilte Programme, die dem Nutzer die Datenanalyse erleichtern.
Von den zahlreichen Untersuchungen der Struktur biologischer Membranen seien nur drei Beispiele erwähnt. Eines ist die Untersuchung der Struktur der Virenschalen und deren Modifikation während der Reifung und aufgrund des Ausstoßes des Genoms. Dieser Fall wird in Aufgabe 35.4 ausführlich behandelt. Als zweites Beispiel betrachten wir kurz die Bestimmung von Phasendiagrammen der Lipid-Legierungen und schließlich die laterale Aggregation von Aktinfilamenten.
Bestimmung der Membranstruktur und der Lipid Phasendiagramme
Die Streuung an Suspensionen von Vesikeln lässt sich auf der Basis des Kratky-Porod-Modells schichtartiger Strukturen analysieren, um die Dicke der Membranen zu bestimmen. Um Phasendiagramme von Lipidmischungen zu bestimmen, deuteriert man eine der Komponenten und versucht den Kontrast der Membranen durch Einstellung des -Gehalts des Wassers anzupassen. Gelingt dies, so sind die Komponenten ideal mischbar. Im Zustand der Entmischung kann man den Kontrast einer der koexistierenden Phasen kompensieren, aber nie beide gleichzeitig. Durch Messung des Kontrasts als Funktion des
-Gehalts des Wasser kann man die Phasengrenze für jede Temperatur bestimmen. Das Verfahren ist sehr mühsam. Es ist aber sehr empfindlich und hat aber den Vorteil, dass man Phasendiagramme im thermodynamischen Gleichgewicht bestimmen kann [3].
Feinstruktur der Aktinbündel
Experimente mit geordneten Stäbchen und Demonstration der Attraktion geladener Makromoleküle durch zweiwertige Ionen (s. Kapitel 36)
Um die Feinstruktur langgestreckter Objekte mittels Kleinwinkelstreuung zu analysieren, muss man diese orientieren. Da man die Strukturfaktoren in Richtung parallel und senkrecht zur Längsachse messen kann, lassen sich durch die Bündelung induzierte Überstrukturen beobachten und analysieren.
Eine interessante Anwendung ist die Untersuchung der Struktur von Aktinbündel, die durch Vernetzer oder zweiwertige Ionen gebildet wurden (s. Kapitel 18). Die ladungsinduzierte Bündelung ist ein schönes Beispiel dafür, dass sich geladene Stäbchen in Gegenwart zweiwertiger Gegenionen anziehen, entgegen der Erwartung nach der Debye-Hückel-Theorie. Im folgenden beschreiben wir ein schöne Experiment von Angelini et al. [5]. Die Filamente wurden in Kapillaren orientiert. Um lange Filamente zu erzeugen, wurden diese mit dem Pilzgift Phalloidin stabilisiert (s. Kapitel 18). Bei niedriger Konzentration zweiwertiger Ionen () bilden sich schwach gekoppelte Bündel, während die Filamente bei etwa 30 mM kondensieren. Die zweiwertigen Ionen bilden dann eine periodische Anordnung in Richtung senkrecht zur Längsachse. Um die elektrostatischen Kopplung zu optimieren, bilden die Filamente eine superverdrillte Struktur. Dies bestätigt die in §36 diskutierte Theorie der Attraktion der Polyelektrolyten durch Ladungsfluktuation zweiwertiger Ionen.
Abb zeigt das Beugungsbild eines geordneten, aber noch locker gepackten Aktinbündels, sowie die Intensitätsverteilungen I(q) in Richtung senkrecht und parallel zur Längsachse. Die Streukurven in z-Richtung zeigt eine 13:6-Symmetrie. Aus dieser erkennt man, dass die Ba-Ionen in 6 Cluster angeordnet sind und die Aktinfilamente eine Superhelix bilden.
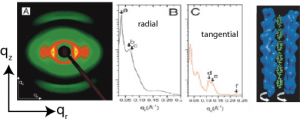
Abb. 37A.4. a) Röntgen Kleinwinkelstreuung (SAXS) von schwach gekoppelten orientierten Aktinbündel. B, C: Intensitätsverteilungen in radialer () und tangentialer Richtung (
).
D) Modell der durch -Ionen kondensierten Filamente. Die grünen Punkte zeigen die strukturierte Ladungswolken der Gegenionen. Man beachte, dass gilt:
,
,
Referenzen:
1 Svergun, D., Koch, M. (2003) Small-angle scattering studies of biological macromolecules in solution Rep. Prog. Phys. 66: 1735
2 Laggner et al. (1977) Hoppe Seylers Zeitschrift für Physiologische Chemie 358: 771
3 G. Porod, Die Röntgenklemwinkelstreuung I. Z Naturforschung 134, 83 (1951)
4 Knoll, W., et al ](1981) Small-Angle Neutron Scattering Study of Lipid Phase Diagrams by the Contrast Variation Method. Biochemistry 20: 6379-6383
5 Angelini, T. et al.(2003) Like-charge attraction between polyelectrolytes”. Proc. Natl. Acad. Sci. USA 100: 8634-8637
